Was ist der Binomialkoeffizient und wie berechnet man ihn?

Binomialkoeffizienten

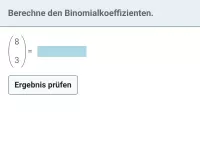
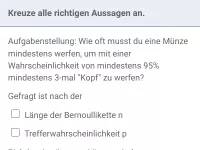
Der Binomialkoeffizient gibt in Bernoulli-Ketten die Anzahl der Pfade an, bei n Durchführungen genau r Treffer zu erhalten.
Dies wird bei der Berechnung von Wahrscheinlichkeiten bei Bernoulli-Ketten benötigt.

Schreibweise:

  • wie ein Vektor (n über r in runden Klammern)
  • Gelesen: "n über r"
Berechnung: mithilfe der nCr-Taste deines Taschenrechners, also zuerst n eingeben, dann nCr-Taste drücken, dann r eingeben. Ohne Taschenrechner:
  • Zähler: n · (n-1) · (n-2) · ... (n-r+1) [insgesamt r Faktoren]
  • Nenner: 1 · 2 · 3 · ... · r [ebenfalls r Faktoren]
  • Kürzen (bis der Nenner 1 ist!), dann verbliebenen Zähler berechnen.
Beispiel
49
7
=
?
Entweder du gibst in deinen Taschenrechner 49 |nCr| 7 ein oder du rechnest zum Beispiel so:
=
49
·
48
·
47
·
46
·
45
·
44
·
43
1
·
2
·
3
·
4
·
5
·
6
·
7
=
7
·
48
·
47
·
46
·
45
·
44
·
43
1
·
2
·
3
·
4
·
5
·
6
·
1
=
7
·
8
·
47
·
46
·
45
·
44
·
43
1
·
2
·
3
·
4
·
5
·
1
·
1
=
7
·
8
·
47
·
46
·
9
·
44
·
43
1
·
2
·
3
·
4
·
1
·
1
·
1
=
7
·
8
·
47
·
46
·
9
·
11
·
43
1
·
2
·
3
·
1
·
1
·
1
·
1
=
7
·
8
·
47
·
46
·
3
·
11
·
43
1
·
2
·
1
·
1
·
1
·
1
·
1
=
7
·
4
·
47
·
46
·
3
·
11
·
43
1
·
1
·
1
·
1
·
1
·
1
·
1
=
7
·
4
·
47
·
46
·
3
·
11
·
43
=
85
 
900
 
584
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen