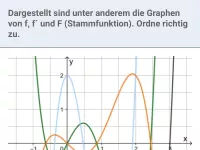
Unter welchen Bedingungen ist eine Funktion an einer Stelle x=a nicht differenzierbar?
Besitzt der Differenzenquotient
[ f(x) − f(a) ] / (x − a)
für x → a (x ≠ a) keinen Grenzwert, so ist f an der Stelle a nicht differenzierbar.Das kann sich beispielsweise darin äußern, dass die einseitigen Grenzwerte nicht übereinstimmen. Der Graph weist an einer solchen Stelle einen Knick auf.
Beispiel
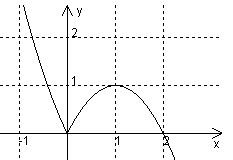
Ist f an der "Nahtstelle" differenzierbar? Bestimme dazu die einseitigen Grenzwerte des Differenzenquotienten.
| = |
|
| = |
|
- x < 0 (links von der Nahtstelle)
| = |
|
Der linksseite Grenzwert
lautet damit
.
|
|
- x > 0 (rechts von der Nahtstelle)
| = |
|
Der rechtsseitige Grenzwert
lautet damit
.
|
2 |
Da linksseitiger und rechtsseitiger Grenzwert voneinander abweichen, ist die Funktion f an der Nahtstelle nicht differenzierbar.
Hinweis: bereits der abgebildete Graph legte diese Vermutung nahe, da er an der Stelle
einen Knick aufweist. Streng genommen lässt sich aber aus dem Aussehen des Graphen keine Aussage über die Differenzierbarkeit ableiten, da sich ein vermeintlicher Knick bei größerer Auflösung auch als abgerundet herausstellen kann.
x | = | 0 |

Lernvideo
Lokales und globales Differenzieren, abschnittsweise definierte Funktion, Beispiel
Kanal: Mathegym
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was zeigt das Vorzeichen der Ableitung f'(x) einer Funktion an?
- Was ist eine Stammfunktion F von f und welche Beziehung besteht zwischen den Werten von f und F?
- Was versteht man unter der "Ableitungskette" in Bezug auf Funktionen und ihre Graphen?
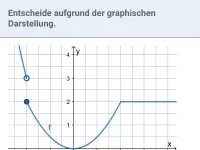
- Wie erkennt man graphisch, dass eine Funktion an einer Stelle nicht differenzierbar ist?
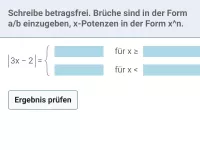
- Wie kann man einen von Betragsstrichen umgebenen Term betragsfrei schreiben?