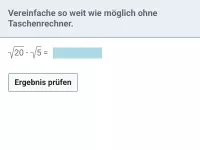
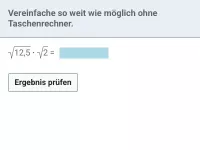
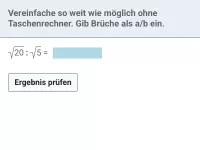
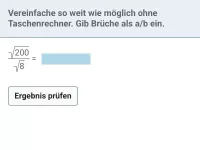
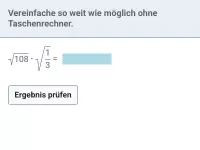
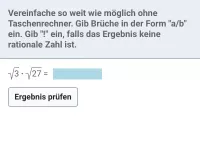
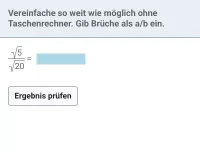
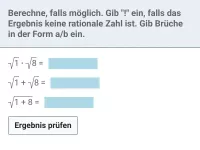
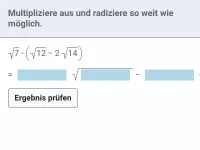
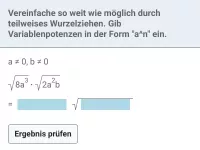
Wie lauten die Rechenregeln für Quadratwurzeln und was bedeutet "teilweise radizieren"?
Ein Produkt von Wurzeln lässt sich als Produkt unter einer Wurzel schreiben und umgekehrt. Sofern weder \(a\) noch \(b\) negativ sind, gilt also
\[ \sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b} \]Ein Quotient von Wurzeln lässt sich als Quotient unter einer Wurzel schreiben und umgekehrt. Sofern weder \(a\) noch \(b\) negativ sind, gilt also
\[ \sqrt{a} : \sqrt{b} = \sqrt{a : b} \]Nach dem Distributivgesetz können gleiche Wurzeln (bzw. Vielfache davon) addiert und subtrahiert werden:
\[ a\sqrt{c} + b\sqrt{c} = (a + b)\sqrt{c} \]Beachte dabei: \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \)
Oft kann man teilweise die Wurzel ziehen. Sofern \(a\) nicht negativ ist, kann man den Faktor \(a^2\) unabhängig vom Faktor \(b\) radizieren:
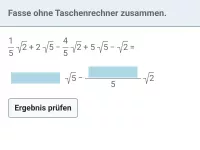
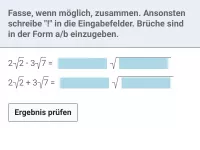
\[ \sqrt{a^2 \cdot b} = \sqrt{a^2} \cdot \sqrt{b} = a \cdot \sqrt{b} \]Beispiel 1
| = | ? |
| = | ? |
| = | ? |
|
= |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
= |
|
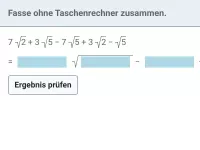
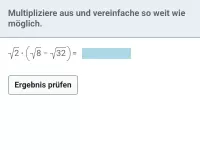
Beispiel 2
| = | ? |
|
= |
|
= |
|
= |
|
= |
|
= |
|
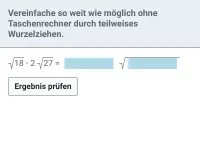
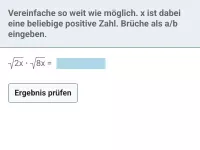
Beispiel 3
| = | ? |
|
= |
|
= |
|
= |
|
= |
|
= |
|
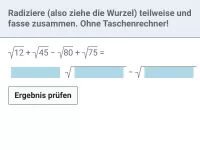
Beispiel 4
| = | ? |
| = | ? |
| = | ? |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
| − |
|
= |
|
= |
|
An diesem Beispiel sieht man sehr schön, dass √a | + | √b ≠ √(a+b) |
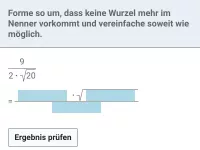
Beispiel 5
| = | ? |
|
|
|
| = |
| Wurzeln zusammenfassen | |||||||||||||||||||||||||||
|
| = |
| kürzen | |||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈9. Klasse - Aufgaben + Stoff + Video
Quadratwurzeln - Grundrechenarten, teilweise radizieren
Teilweises Wurzelziehen; Produkte, Summen und Differenzen aus Wurzeltermen vereinfachen -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratwurzeln - Termumformung ohne Binomische Formeln
Rechnen mit Quadratwurzeln unter Anwendung des D-Gesetzes, auch mit Variablen
Ähnliche Themen
- Was besagt das Distributivgesetz in der Mathematik?
- Wie funktioniert die Addition und Subtraktion von Quadratwurzeln?
- Wie funktioniert die Multiplikation und Division von Quadratwurzeln und was versteht man unter teilweisem Radizieren?
- Wie kann man \( \sqrt{a^2} \) vereinfachen, wenn a auch negativ sein könnte?
- Was bedeutet Rationalmachen des Nenners und wie wird es durchgeführt?
- Was bedeutet die Normalform eines Wurzelterms?