Was besagt der Satz des Thales und was ist ein Thaleskreis?
Satz des Thales:
- Liegen A, B und C auf einem Kreis und geht [AB] durch den Mittelpunkt, so ist das Dreieck ABC bei C rechtwinklig. Man spricht vom "Thaleskreis" über [AB].
- Umgekehrt gilt: ist das Dreieck ABC bei C rechtwinklig, so liegt C auf dem Thaleskreis über [AB].
Beispiel 1
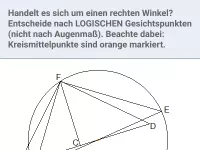
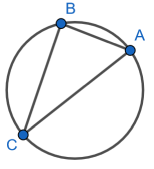
Welche der folgenden Dreiecke sind rechtwinklig?
|  |
Lösung:
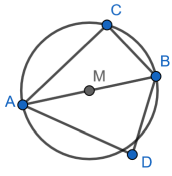
- Figur links
Δ ABC ist rechtwinklig, da C auf dem Thaleskreis über [AB] liegt.
Δ BAD ist bei D nicht rechtwinklig, da D nicht auf dem Thaleskreis über [AB] liegt.
Δ BAD ist bei D nicht rechtwinklig, da D nicht auf dem Thaleskreis über [AB] liegt.
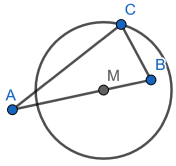
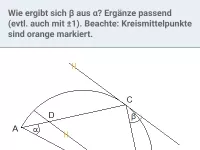
- Figur mitte
Δ ABC könnte bei C rechtwinklig sein - und zwar dann, wenn C auf dem Thaleskreis über [AB] liegt.
Bemerkung: der abgebildete Kreis ist nicht der Thaleskreis über [AB], weil er nicht durch A und B geht. Dass er zufällig durch C geht, tut nichts zur Sache.
Bemerkung: der abgebildete Kreis ist nicht der Thaleskreis über [AB], weil er nicht durch A und B geht. Dass er zufällig durch C geht, tut nichts zur Sache.
- Figur rechts
Δ CAB könnte bei B rechtwinklig sein - und zwar dann, wenn [CA] durch den Mittelpunkt des Kreises geht; dann wäre der Kreis nämlich der Thaleskreis über [CA].

Lernvideo
Thaleskreis, Beispiel
Kanal: Mathegym Basics
Beispiel 2
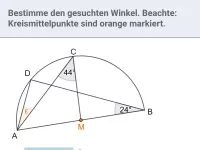
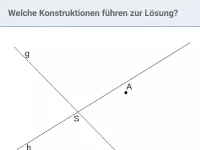
Ermittle durch Konstruktion alle Punkte, von denen aus die beiden Strecken a und b unter einem rechten Winkel erscheinen.
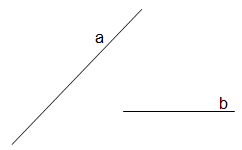
Lösung: Auf dem Thaleskreis über a liegen alle Punkte, von denen aus a unter einem rechten Winkel erscheint. Auf dem Thaleskreis über b liegen alle Punkte, von denen aus b unter einem rechten Winkel erscheint. Die Schnittpunkte beider Thalskreise (R und S) sind damit die Lösung. Zum besseren Verständnis ist bei R der rechte Winkel durch die orangen Linien verdeutlicht:
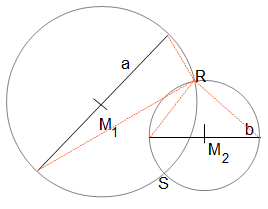
Konstruktionsschritte:
- Mittelsenkrechte über a geschnitten mit a ergibt M1
- Mittelsenkrechte über b geschnitten mit b ergibt M2
- Thaleskreis über a mit Mittelpunkt M1
- Thaleskreis über b mit Mittelpunkt M2
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈7. Klasse - Aufgaben + Stoff + Video
Dreiecke - rechtwinklig
Satz des Thales und Anwendungen, u.a. Konstruktion von rechtwinkligen Dreiecken und Kreistangenten sowie sowie Bestimmung von Winkelgrößen in Drei- und Vielecken -
≈7. Klasse - Aufgaben + Stoff
Konstruktion mit Zirkel und Lineal - Standardkonstruktionen
Mittelsenkrechte, Winkelhalbierende, Lot, Höhe, Inkreis, Umkreis, Höhenschnittpunkt, Thaleskreis