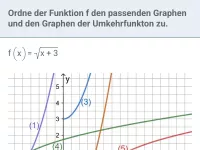
Wie bestimmt man den Term der Umkehrfunktion einer umkehrbaren Funktion?
Ist eine Funktion umkehrbar, so erhält man den Term der Umkehrfunktion nach folgendem Rezept:
- Löse die Gleichung y = f(x) nach x auf.
- Vertausche dann x und y.
Beispiel
| = |
|
Gib den Term der Umkehrfuktion
an.
|
|
- Formelle Lösung
Löse die Gleichung nach x auf und vertausche am Ende x und y:
| = |
|
| ||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
| x und y vertauschen | ||||||||||||||||||||
| = |
| |||||||||||||||||||||
| = |
| |||||||||||||||||||||
- Intuitive Lösung
Der gegebene x-Wert wird in
zunächst mit −0,5 multipliziert, zum Ergebnis wird
addiert. Um diesen Prozess rückgängig zu machen (Umkehrfunktion), müsste man also mit dem Endergebnis folgendes machen: zuerst
wieder subtrahieren, das Ergebnis dann durch
teilen (oder mit -2 multiplizieren).
f |
|
1 |
9 |
1 |
9 |
− | 0,5 |
| = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Potenzfunktionen - rationaler Exponent
Definitionsmenge, Graph und Umkehrfunktion von Potenzfunktionen mit rationalem Exponent -
≈Oberstufe - Aufgaben + Stoff + Video
Umkehrfunktionen
Graph, Term und Definitionsmenge der Umkehrfunktion bestimmen; auf Umkehrbarkeit prüfen bzw. Definitionsmenge entsprechend einschränken
Ähnliche Themen
- Wie hängt die maximale Definitionsmenge einer Potenzfunktion von ihrem Exponenten ab?
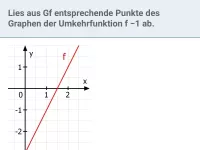
- Wie kann man den Graphen und die Wertemenge einer Umkehrfunktion beschreiben?
- Welche Klassen von Potenzfunktionen f(x) = x^r, r ∈ ℚ, lassen sich graphisch unterscheiden?
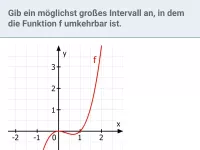
- Wie kann man feststellen, ob eine Funktion umkehrbar ist?