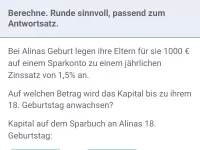
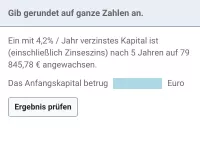
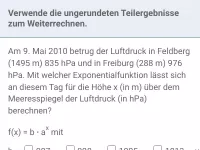
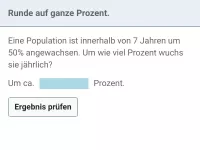
Wie hängen Wachstumsrate und Wachstumsfaktor beim exponentiellen Wachstum zusammen?

Wachstumsrate = Wachstumsfaktor a − 1
  • Nimmt ein Bestand pro Zeitschritt um 20% (= Rate) zu, so hat er sich auf 120% (= a) des ursprünglichen Bestands vergößert.
  • Nimmt ein Bestand pro Zeitschritt um 20% (Rate) ab, so hat er sich auf 80% (= a) des ursprünglichen Bestands verringert.
Ansonsten bedenke, dass 80% = 0,8 und 120% = 1,2.
Beispiel
Wie lautet der Wachstumsfaktor (bezogen auf das angegebene Zeitintervall)
  1. bei einer monatlichen Zunahme um die Hälfte
  2. bei einer jährlichen Abnahme um ein Viertel
  3. bei einem täglichen Rückgang um 1,5%
Lösung:
a) 
100%
+
50%
=
150%
=
1,5
b) 
100%
−
25%
=
75%
=
0,75
b) 
100%
−
1,5%
=
98,5%
=
0,985
Exponentielles Wachstum, Wachstumsfaktor, Beispiel 2
Lernvideo

Exponentielles Wachstum, Wachstumsfaktor, Beispiel 2

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen