Was ist der allgemeine Term einer Exponentialfunktion und welche Bedeutung haben die Parameter?

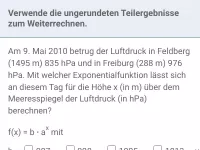
Funktionen mit der Gleichung f(x) = b · ax heißen Exponentialfunktionen. Dabei ist
  • a > 0 der Wachstumsfaktor und
  • b = f(0) der Anfangsbestand
Beispiel 1
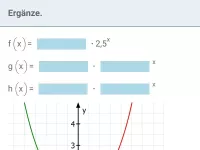
Schreibe in der Form 
f
 
x
=
b
·
a
x
.
f
 
x
=
1
5
6
·
2
1
−
x
1
5
6
·
2
1
−
x
=
1
5
6
·
2
1
·
2
−
x
1. Potenzgesetz
=
1
5
6
·
2
·
2
−
x
=
2
10
6
·
0,5
x
=
3
2
3
·
0,5
x
Erläuterung zur dritten Zeile: 
a
−
x
=
1
a
x
=
1
a
x
 solltest du dir als Formel merken, das braucht man sehr oft.
Exponentielles Wachstum, Beispiel Funktionsterm vereinfachen
Lernvideo

Exponentielles Wachstum, Beispiel Funktionsterm vereinfachen

Kanal: Mathegym
Beispiel 2
Ein zu festem Jahreszinssatz angelegtes Kapital ist innerhalb von 10 Jahren auf 300% angewachsen. Wie hoch ist der Zinsatz?
Lösung siehe Video:
Exponentielles Wachstum, Funktionsterm bestimmen, Beispiel 2
Lernvideo

Exponentielles Wachstum, Funktionsterm bestimmen, Beispiel 2

Kanal: Mathegym
Beispiel 3
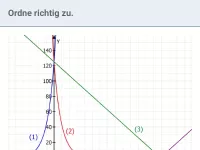
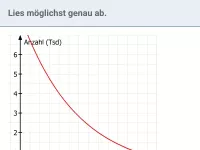
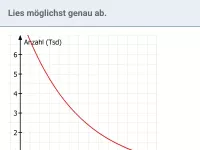
Gegeben ist der Graph einer Exponentialfunktion mit der Gleichung 
y
=
b
·
a
x
. Bestimme a und b.
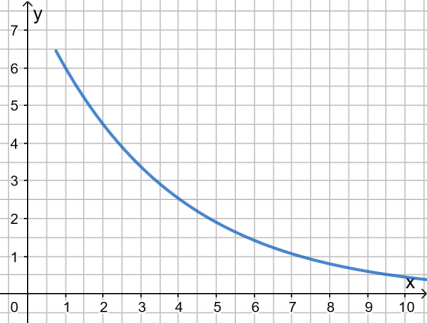
graphik
  • Punkte ablesen und einsetzen
Man kann aus dem Diagramm die Punkte (1|6) und (2|4,5) ablesen. Setzt man in die Gleichung für x und y jeweils die Koordinaten dieser Punkte  ein, so erhält man die beiden Gleichungen:
I
 
6
=
b
·
a
1
II
 
4,5
=
b
·
a
2

  • Gleichungssystem lösen
Um eine Unbekannte zu eliminieren, kann man hier die zweite Gleichung durch die erste teilen; dadurch fällt b weg und man erhält a:
II
:
I
 
4,5
6
=
b
·
a
2
b
·
a
kürzen
3
4
=
a
Jetzt kann man 
a
=
3
4
 in eine der beiden Gleichungen, z.B. die erste einsetzen und nach b auflösen:
I
 
6
=
b
·
3
4
·
4
3
8
=
b
Exponentielles Wachstum, Funktionsterm bestimmen, Beispiel 1
Lernvideo

Exponentielles Wachstum, Funktionsterm bestimmen, Beispiel 1

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen