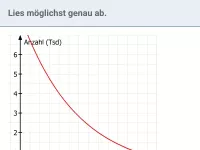
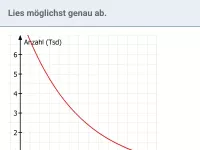
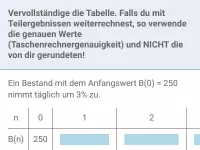
Was ist bei linearem und exponentiellem Wachstum jeweils konstant und wie erkennt man dies in einer Wertetabelle?

Beim linearen Wachstum ist der absolute Zuwachs in gleichen Zeitschritten konstant, d.h.
  f(t+1) − f(t) = d (absolute Zunahme pro Zeitschritt)

Beim exponentiellen Wachstum ist der relative Zuwachs konstant, d.h.
  f(t+1) : f(t) = a (Wachstumsfaktor)

Bezogen auf eine Wertetabelle heißt das:
  • Bei linearem Wachstum ist die Differenz benachbarter Funktionswerte konstant.
  • Bei exponentiellem Wachstum ist der Quotient benachbarter Funktionswerte konstant.
Unterscheide zwischen Wachstum (d > 0 bzw. a > 1) und Abnahme (d < 0 bzw. 0 < a < 1)
Beispiel 1
Handelt es sich um lineares oder exponentielles Wachstum (oder weder noch)?
a
    
x
1
2
3
4
5
y
1
3
2
3
1
1
3
2
2
3
5
1
3
b
    
x
1
2
3
4
5
y
1
3
1
2
3
3
4
1
3
6
  • Lösung zu a)
Überprüfe auf geiche y-Differenzwerte (bei gleichmäßigen x-Schritten):
2
3
−
1
3
=
1
3
1
1
3
−
2
3
=
2
3
Bereits hier kann man abbrechen, da die Differenzwerte nicht übereinstimmen. Lineares Wachstum scheidet also aus.
Überprüfe auf gleiche y-Quotienten (bei gleichmäßigen x-Schritten):
2
3
:
1
3
=
2
1
1
3
:
2
3
=
2
2
2
3
:
1
1
3
=
2
5
1
3
:
2
2
3
=
2
Pro Zeitschritt wird der y-Wert mit 2 multipliziert. Also handelt es sich um exponentielles Wachstum (mit Wachstumsfaktor 2).

  • Lösung zu b)
Überprüfe auf geiche Differenzwerte:
1
2
3
−
1
3
−
=
1
1
3
3
−
1
2
3
=
1
1
3
4
1
3
−
3
=
1
1
3
6
−
4
1
3
=
1
2
3
Der letzte Differenzwert stimmt nicht mit den anderen überein. Lineares Wachstum scheidet also aus. Da y mehrmals hintereinander um den selben Betrag 
1
1
3
 anwächst, scheidet aber auch exponentielles Wachstum aus, denn bei diesem müssten von Schritt zu Schritt immer größere Diffenzwerte herauskommen. Man kann das natürlich auch wie sonst anhand der Quotientenwerte überprüfen, aber eigentlich ist dieser Schritt nicht mehr nötig:
1
2
3
:
1
3
=
5
3
:
1
2
3
=
9
5
Es liegt weder lineares noch exponentielles Wachstum vor.
Exponentielles Wachstum, Beispiel Überprüfung (linear/exponentiell)
Lernvideo

Exponentielles Wachstum, Beispiel Überprüfung (linear/exponentiell)

Kanal: Mathegym
Zeige, dass exponentielles Wachstum vorliegt
Lernvideo

Zeige, dass exponentielles Wachstum vorliegt

Kanal: Formelfabrik - Mathenachhilfe
Beispiel 2
Ergänze so, dass es sich um exponentielles Wachstum handelt.
x
1
2
3
4
5
y
5
7
?
?
0,245
?
Da zwischen 
y
=
5
7
 und 
y
=
0,245
 drei Zeitschritte liegen, gilt für den Wachstumsfaktor a:
5
7
·
a
3
=
0,245
:
5
7
a
3
=
0,343
3
 
a
=
0,7
Berechne damit die fehlenden y-Werte:
5
7
·
0,7
=
0,5
    
x
=
2
0,5
·
0,7
=
0,35
    
x
=
3
0,245
·
0,7
=
0,1715
    
x
=
5
x
1
2
3
4
5
y
5
7
0,5
0,35
0,245
0,1715
Exponentielles Wachstum, Wachstumsfaktor, Beispiel 1
Lernvideo

Exponentielles Wachstum, Wachstumsfaktor, Beispiel 1

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen