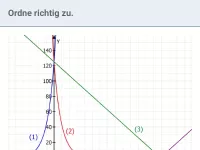
Wie beeinflussen die Parameterwerte den Verlauf des Graphen einer Exponentialfunktion?
Der Graph einer Exponentialfunktion mit der Gleichung y = b · ax hat stets die x-Achse als Asymptote und schneidet die y-Achse in (0|b).
Im Fall b > 0
- steigt der Graph für a > 1 ("ins Unendliche")
- fällt der Graph für 0 < a < 1
Im Fall b < 0 (Spiegelung an der x-Achse gegenüber dem positiven Betrag von b) verhält es sich genau umgekehrt.
Beispiel
Für welche Werte von a
(a) fällt der Graph von f(x) | = |
|
(b) steigt der Graph von f(x) | = |
|
Lösung siehe Video:

Lernvideo
Exponentielles Wachstum, Beispiel Parameterbestimmung
Kanal: Mathegym
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was ist bei linearem und exponentiellem Wachstum jeweils konstant und wie erkennt man dies in einer Wertetabelle?
- Was sind Halbwertszeit und Verdoppelungszeit und wie werden sie definiert?
- Was ist der allgemeine Term einer Exponentialfunktion und welche Bedeutung haben die Parameter?
- Was sind die konstanten Faktoren und Funktionsterme bei linearem und exponentiellem Wachstum?
- Wie beeinflussen die Werte von a und b sowie ihre Modifikationen den Graphen der Funktion f(x) = b*a^x?