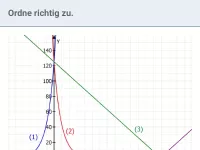
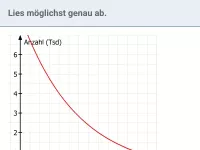
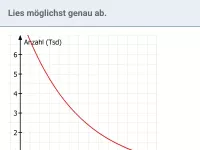
Was sind die konstanten Faktoren und Funktionsterme bei linearem und exponentiellem Wachstum?

Sei B(n) der Bestand nach dem n-ten Zeitschritt.
Unterscheide zwischen linearem und exponentiellem Wachstum:
  • Linear: Zunahme pro Zeitschritt ist - absolut - immer gleich, d.h.
    B(n + 1) = B(n) + d
    Den Bestand nach n Zeitschritten berechnet man mithilfe der Formel:
    B(n) = B(0) + n ·d
    d bezeichnet hier die Änderung pro Zeitschritt.
  • Exponentiell: Zunahme pro Zeitschritt ist - prozentual - immer gleich, d.h.
    B(n + 1) = B(n) · k.
    Den Bestand nach n Zeitschritten berechnet man mithilfe der Formel:
    B(n) = B(0) ·kn
    k bezeichnet hier den Wachstumsfaktor.
Beispiel
  • Exponentielles Wachstum
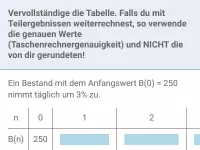
Ein Bestand mit dem Anfangswert B(0) = 1000 nimmt täglich um 2,5% zu.
n
0
1
2
5
10
B(n)
1000
?
?
?
?
  • Lineares Wachstum
Ein Bestand mit dem Anfangswert B(0) = 1000 nimmt täglich um 25 zu.
n
0
1
2
5
10
B(n)
1000
?
?
?
?
  • Exponentielles Wachstum
In jedem Zeitschritt ist die prozentuale Änderung gleich.
Der Wachstumsfaktor ist:
k
=
1
+
p
=
1
+
0,025
=
1,025
Hinweis: Würde der Bestand täglich um 2,5% abnehmen, wäre der Wachstumsfaktor:
k
=
1
+
p
=
1
+
−
0,025
=
0,975
Es gilt:
B(n)
=
B(0)
·
1,025
n
B(1)
=
1000
·
1,025
1
=
1025
B(2)
=
1000
·
1,025
2
=
1050,625
 
≈
 
1050,63
B(5)
=
1000
·
1,025
5
 
≈
 
1131,41
B(10)
=
1000
·
1,025
10
 
≈
 
1280,08
n
0
1
2
5
10
B(n)
1000
1025
1050,63
1131,41
1280,08
  • Lineares Wachstum
In jedem Zeitschritt ist die absolute Änderung gleich.
Da der Bestand zunimmt, ist:
d
=
25
Hinweis: Würde der Bestand abnehmen, wäre:
d
=
−
25
Es gilt:
B(n)
=
B(0)
+
n
·
d
B(1)
=
1000
+
1
·
25
=
1025
B(2)
=
1000
+
2
·
25
=
1050
B(5)
=
1000
+
5
·
25
=
1125
B(10)
=
1000
+
10
·
25
=
1250
n
0
1
2
5
10
B(n)
1000
1025
1050
1125
1250
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen