Was bleibt beim exponentiellen Wachstum gleich und wie geht man bei typischen Fragestellungen vor?
Exponentielles Wachstum:
Zunahme pro Zeitschritt ist - prozentual - immer gleich, d.h.
B(n + 1) = B(n) · k.
Zunahme pro Zeitschritt ist - prozentual - immer gleich, d.h.
B(n + 1) = B(n) · k.
- B(n) gesucht: Den Bestand nach n Zeitschritten berechnet man mithilfe der Formel:
- n gesucht: Ist n gesucht, löst man die Formel nach n auf:
- B(0) gesucht: Ist B(0) gesucht, löst man die Formel nach B(0) auf:
- k gesucht:
Ist k gesucht, löst man die Formel nach k auf:
B(n) = B(0) · kn | : B(0)
B(n) / B(0) = kn
Zuletzt zieht man noch die n-te Wurzel
B(n) = B(0) · kn
B(n) = B(0) · kn | : B(0)
B(n) / B(0) = kn | log
log( B(n) / B(0) ) = log( kn)
log( B(n) / B(0) ) = n · log( k ) | : log( k )
n = log( B(n) / B(0) ) / log( k )
B(n) = B(0) · kn | : kn
B(0) = B(n) / kn
Beispiel 1
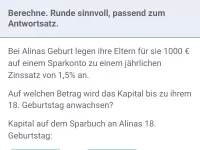
Ein Kapital von 2000 € vermehrt sich auf einem Sparkonto pro Jahr um 0,1%.
Nach 8 Jahren beträgt das Kapital auf dem Konto:
| Cent |
B(0) | = | 2000 |
n | = | 8 |
| = | 1,001 |
B(n) | = |
|
B(8) | = |
|
| 2016,06 |
Nach 8 Jahren befinden sich 2016 Euro und 6 Cent auf dem Sparkonto.
Beispiel 2
Ein Guthaben von 5000 € wird mit 3,7% verzinst. Nach wie vielen Jahren ist es auf 8000 € angewachsen?
Nach ? Jahren beträgt das Guthaben 8000 €.
B(0) | = | 5000 |
| = |
|
B(n) | = | 8000 |
B(n) | = |
|
| = |
|
| ||||||||||
| = |
| log | ||||||||||
| = |
| |||||||||||
| = |
|
| ||||||||||
| = |
| |||||||||||
| 12,93637962 |
Gerundet auf die 2. Dezimale:
|
n liegt zwischen 12 und 13. Nach 12 Jahren beträgt das Kapital noch nicht ganz 8000 €. Nach 13 Jahren ist das Guthaben auf etwas mehr als 8000 € angewachsen.
B(12) ≈ 7732,41 €
B(13) ≈ 8018,51 €
Zur Beantwortung der Aufgabe wird auf Ganze gerundet:
Das heißt, dass das Anfangskapital nach 13 Jahren auf 8000 € angewachsen sein wird.
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈10. Klasse - Aufgaben + Stoff + Video
Exponentielles Wachstum - Anwendungen
Exponentielles Wachstum im Sachzusammenhang, Sachaufgaben -
≈10. Klasse - Aufgaben + Stoff + Video
Exponentielles Wachstum/Exponentialfunktion
Unterscheidung zwischen linearen und exponentiellen Wachstumsvorgängen, Parameter exponentiellen Wachstums, Exponentialfunktion (inkl. Graph), Bestimmung von Anfangsbestand und Wachstumsfaktor
Ähnliche Themen
- Was ist bei linearem und exponentiellem Wachstum jeweils konstant und wie erkennt man dies in einer Wertetabelle?
- Wie hängen Wachstumsrate und Wachstumsfaktor beim exponentiellen Wachstum zusammen?
- Was sind Halbwertszeit und Verdoppelungszeit und wie werden sie definiert?
- Wie beeinflussen die Parameterwerte den Verlauf des Graphen einer Exponentialfunktion?
- Was ist der allgemeine Term einer Exponentialfunktion und welche Bedeutung haben die Parameter?
- Wie beschreibt man die Änderung des Bestandes bei einem Wachstumsvorgang von einem Zeitschritt zum nächsten?
- Was sind die konstanten Faktoren und Funktionsterme bei linearem und exponentiellem Wachstum?
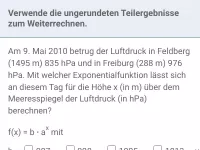
- Wie beeinflussen die Werte von a und b sowie ihre Modifikationen den Graphen der Funktion f(x) = b*a^x?