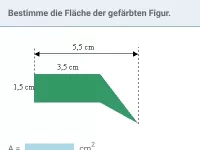
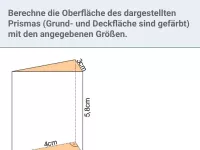
Wie berechnet man Fläche und Umfang eines Dreiecks?
Ein Dreieck mit den Seitenlängen a, b und c
und den zugehörigen Höhen ha, hb und hc hat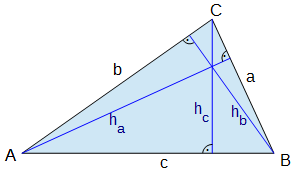
und den zugehörigen Höhen ha, hb und hc hat
- den Umfang U = a + b + c
- den Flächeninhalt A = ½ · a · ha = ½ · b · hb = ½ · c · hc

Achte bei der Rechnung darauf, dass alle Größen in derselben Einheit angegeben sind (evtl. umwandeln!)
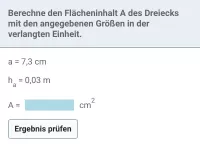
Beispiel 1
| = |
|
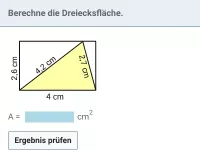
Gesucht sind die Fläche A und der Umfang U.
Lösung:
Flächeninhalt A | = |
- Formel für das Dreieck
| = |
| = |
- gleiche Einheit (cm) für Rechnung
| = |
| = |
| = |
- Umwandlung in die geforderte Einheit
|
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Umfangs U | = |
- Formel für das Dreieck
| = |
| = |
- gleiche Einheit (cm) für Rechnung
| = |
166 cm | = |
- Umwandlung in geforderte Einheit
16,6 dm |
Beispiel 2
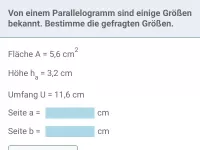
Gegeben ist ein Dreieck mit folgenden (gerundeten) Angaben:
| ; |
|
Bestimme daraus die Seiten a, b und c.
Lösung: Die Seiten b und c können mit Hilfe der Flächenformel bestimmt werden, weil die Fläche und die jeweiligen Höhen gegeben sind. Danach kann a mithilfe der Umfangsformel bestimmt werden.
- - - - - - - - - - Bestimmung von b:
A | = |
|
| = |
|
| = |
|
b durch Division:
|
|
- - - - - - - - - - Bestimmung von c:
A | = |
|
| = |
|
| = |
|
c durch Division:
|
|
- - - - - - - - - - Bestimmung von a:
U | = |
|
20,6 cm | = |
|
20,6 cm | = |
|
a durch Subtraktion:
| = |
|