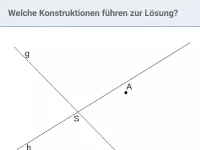
Welche exklusive Eigenschaft haben die Punkte, die auf der Mittelsenkrechten einer Strecke AB liegen, bzgl. der Punkte A und B? Was heißt in diesem Zusammenhang "exklusiv"?
Punkte, die auf der Mittelsenkrechten einer Strecke AB liegen, haben eine exklusive Eigenschaft (d.h. nur sie haben diese Eigenschaft): Sie sind zu A und B gleich weit entfernt. D.h.
- ist P ein beliebiger Punkt der Mittelsenkrechten, so ist dieser zu A und B gleich weit entfernt.
- ist irgendein Punkt P von A und B gleich weit entfernt, so muss die Mittelsenkrechte durch P gehen (darum "exklusiv").
Beispiel 1
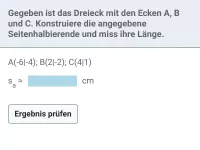
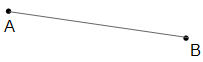
Gegeben ist die Strecke AB. Konstruiere die Mittelsenkrechte.
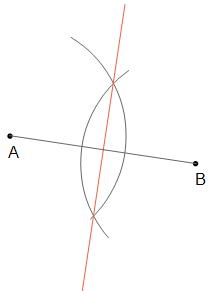
Lösung: Man zeichnet zwei gleich große Kreise um A und B, die sich schneiden. Diese Schnittpunkte haben jeweils von A und B die gleiche Entfernung und müssen daher auf der Mittelsenkrechten liegen.
Beispiel 2
Ein Winkel soll halbiert werden.
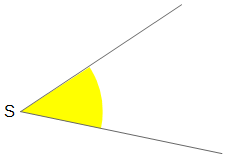
Lösung:
- Ziehe einen Kreis um den Scheitelpunkt, dieser schneide die beiden Schenkel in den Punkten A und B.
- Ziehe zwei gleich große Kreise um A und um B. Durch deren Schnittpunkt C verläuft die Winkelhalbierende.
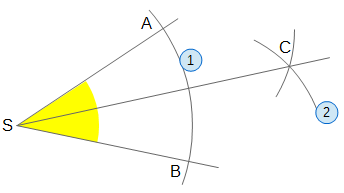
Begründung für das Vorgehen: SC ist die Mittelsenkrechte der Strecke AB.
Beispiel 3
Im Punkt P soll ein Lot zur Geraden g errichtet werden.

Lösung:
- Ziehe einen Kreis um P, so dass dieser die Gerade g in zwei Punkten A und B schneidet.
- Ziehe zwei gleich große Kreise um A und um B. Durch deren Schnittpunkt C verläuft das Lot.
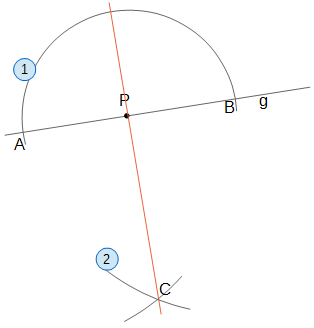
Begründung für das Vorgehen: Man konstruiert die Mittelsenkrechte von AB; diese geht durch P, da P der Mittelpunkt von AB ist.
- - - - - - - - - - - - - - - - - - - - -
P muss für diese Konstruktion nicht auf g liegen, d.h. genauso wie oben kann man vorgehen, wenn von P aus ein Lot auf g gefällt werden soll. In diesem Fall kann man es sich allerdings noch einfacher machen:
- Wähle zwei Punkte A und B auf g.
- Ziehe um A und B jeweils einen Kreis durch P. Das Lot verläuft durch die Kreisschnittpunkte.
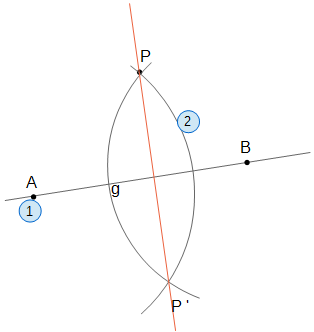
Begründung für das Vorgehen: A und B sind von P und P´ jeweils gleich weit entfernt, also ist AB die Mittelsenkrechte von PP´.
Beispiel 4
Gegeben ist das folgende Dreieck. Konstruiere den Höhenschnittpunkt.
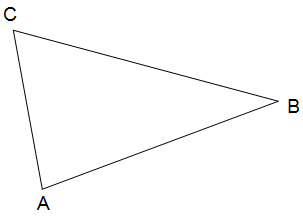
Lösung: Um z.B. die Höhe hc zu konstruieren, also die Höhe durch C, die auf der gegenüberliegenden Seite c senkrecht steht, zeichnet man einen Kreis um C, der die Gerade AB in zwei Punkten schneidet und konstruiert dann die Mittelsenkrechte bezüglich der Verbindungsstrecke beider Schnittpunkte.
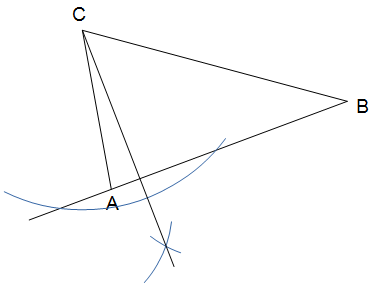
Analog verfährt man, um z.B. die Höhe ha zu konstruieren, also die Höhe durch A, die auf der gegenüberliegenden Seite a senkrecht steht.
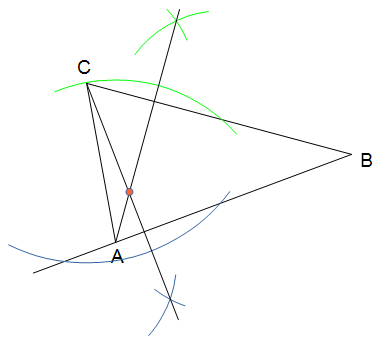
Der Punkt, in dem sich die beiden Höhen schneiden, ist der "Höhenschnittpunkt".
Siehe auch