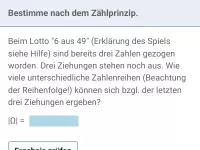
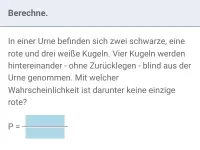
Wie kann das Zählprinzip bei mehrstufigen Zufallsexperimenten angewendet werden? Erkläre dies an einem Beispiel.

Setzt sich ein Zufallsexperiment aus mehreren Stufen zusammen (z.B. dreimal hintereinander Würfeln oder sechs Kugeln hintereinander aus einer Urne ziehen) und hängt die Anzahl der Möglichkeiten auf jeder Stufe nicht davon ab, was auf einer vorangegangenen Stufe gezogen wurde, so lässt sich die Anzahl aller Versuchsausgänge mit dem sogenannten Zählprinzip bestimmen: Betrachte dazu auf jeder Stufe die Anzahl der Möglichkeiten und multipliziere diese Zahlen miteinander.

Oft entstehen hierbei Produkte der Art n·(n-1)·(n-2)·...·2·1; dafür gibt es die abkürzende Schreibweise n! ("n-Fakultät").

Beispiel

Eine vierstellige Zahl soll durch einen Zufallsgenerator erzeugt werden, wobei folgende Vorgaben gemacht werden: an der ersten und dritten Stelle muss eine gerade Ziffer stehen, an der zweiten Stelle eine durch 3 teilbare Ziffer und an letzter Stelle eine Ziffer kleiner als 7. Wie viele Ergebnisse sind möglich?

Lösung:

Für die erste Ziffer stehen 2, 4, 6 und 8, also vier Möglichkeiten zur Auswahl (0 kommt nicht in Frage, denn dann wäre die Zahl nicht vierstellig)

Für die zweite Ziffer stehen 3, 6 und 9, also drei Möglichkeiten zur Auswahl.

Für die dritte Ziffer stehen 0, 2, 4, 6 und 8, also fünf Ziffern zur Auswahl.

Für die letzte Ziffer stehen 0, 1, … 6, also sieben Ziffern zur Auswahl.

Nach dem Zählprinzip ergeben sich damit

420

mögliche Zahlen.

Erläuterung: warum werden die Zahlen multipliziert und nicht addiert? Stelle dir dazu ein Baumdiagramm vor: es beginnt mit vier Ästen; von jedem dieser vier Äste gehen jeweils drei Äste weg usw.

Siehe auch