Welche vier Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
Folgende Ausnahmefälle hinsichtlich der Lage zweier Geraden sind zu beachten:
- Beide Geraden sind (echt) parallel, haben also keinen Schnittpunkt. Das passiert, wenn beide Geraden dieselbe Steigung, aber unterschiedliche y-Achsenabschnitte haben. In dem Fall lässt sich die Gleichung g(x) = h(x) nicht lösen, es entsteht eine falsche Aussage wie z.B. 1=0.
- Beide Geraden sind identisch, zu erkennen an derselben Steigung und demselben y-Achsenabschnitt. Die Gleichung g(x) = h(x) beschreibt in diesem Fall eine wahre Aussage wie z.B. 0 = 0, hat also unendlich viele Lösungen.
- Eine Geraden ist senkrecht, z.B. x = 5; dann kann die andere Gerade sie, wenn überhaupt, nur bei x = 5 schneiden.
- Eine Geraden ist waagrecht, z.B. y = 5; dann kann die andere Gerade sie, wenn überhaupt, nur in (?|5) schneiden.
Beispiel
f: y | = |
|
g: x | = | 4 |
h: y | = | 3 |
i: y | = | 0,125x |
Untersuche paarweise, wie die Geraden zueinander liegen und bestimme gegebenenfalls den Schnittpunkt.
- f und g
Bei g handelt es sich um den Sonderfall einer senkrechten Geraden (parallel zur y-Achse); f und g schneiden sich also bei
. Den y-Wert des Schnittpunkts erhält man durch Einsetzen:
. Also schneiden sich f und g in S1(4|2,5).
x | = | 4 |
| = | 2,5 |
- f und h
Bei h handelt es sich um den Sonderfall einer waagrechten Geraden (parallel zur x-Achse). Den x-Wert des Schnittpunkts erhält man wie üblich durch Gleichsetzen beider Terme:
| = |
|
| ||||||||||||
| = |
|
| ||||||||||||
| = |
| |||||||||||||
Der y-Wert muss natürlich 3 sein, d.h. beide Geraden schneiden sich in S2(8|3).
- f und i
f und i haben beide die Steigung 0,125 und sind damit parallel. An den y-Achsenabschnitten erkennt man, ob sie echt parallel oder aufeinanderliegend, also unecht parallel, sind. Da beide Geraden die y-Achse in unterschiedlichen Punkten schneiden, sind die Geraden f und i echt parallel.
- g und h
...stehen senkrecht aufeinander und schneiden sich in S3(4|3).
- g und i
| = | 0,5, |
- h und i
| = |
|
| |||||||
| = |
| ||||||||
Beide Geraden schneiden sich somit in S5(24|3).
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
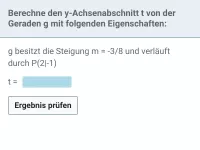
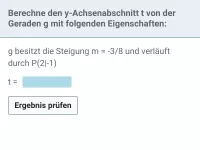
- Wie berechnet man den y-Achsenabschnitt einer Geraden, wenn die Steigung und ein Punkt bekannt sind?
- Wie berechnet man die Steigung einer Geraden mit zwei gegebenen Punkten?
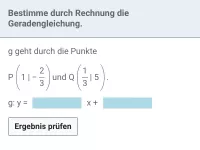
- Wie bestimmt man die Gleichung einer Geraden aus zwei gegebenen Punkten?
- Wie bestimmt man die Steigung einer Geraden mit bekanntem y-Achsenabschnitt und einem weiteren Punkt?
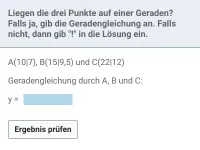
- Wie prüfst du rechnerisch, ob drei Punkte auf einer Geraden liegen?