Wie prüfst du rechnerisch, ob drei Punkte auf einer Geraden liegen?
Liegen drei Punkte auf einer Geraden?
Sind drei Punkte A(xA|yA), B(xB|yB) und C(xC|yC) gegeben, dann stelle eine Geradengleichung durch zwei Punkte, etwa A und B auf:
y = m⋅x + t
Setze dann Punkt C ein:
yC = m⋅xC + t
Erhältst du rechts und links vom Gleichheitszeichen die gleiche Zahl, liegen die drei Punkte auf einer Geraden, ansonsten nicht.
Sind drei Punkte A(xA|yA), B(xB|yB) und C(xC|yC) gegeben, dann stelle eine Geradengleichung durch zwei Punkte, etwa A und B auf:
- Berechne Δy = yB − yA und Δx = xB − xA
- Berechne Steigung m = Δy/Δx
- Berechne y-Achsenabschnitt t = yA − m⋅xA
y = m⋅x + t
Setze dann Punkt C ein:
yC = m⋅xC + t
Erhältst du rechts und links vom Gleichheitszeichen die gleiche Zahl, liegen die drei Punkte auf einer Geraden, ansonsten nicht.
Beispiel
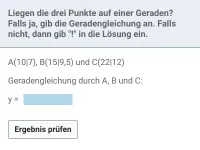
Liegen die drei Punkte auf einer Geraden?
A(1|2), B(3|8) und C(4|9)
Geradengleichung durch A und B:
Steigung m berechnen:
| = | 6 |
| = | 2 |
| = | 3 |
m in die Geradengleichung einsetzen:
y | = |
|
Punkt A (oder B) in Geradengleichung einsetzen:
2 | = |
|
Nach t umstellen:
| = |
|
| |||||||
| = |
| ||||||||
Geradengleichung durch A und B:
y | = |
|
Punkt C einsetzen:
| = |
| |||||||||
| = |
| |||||||||
| = |
| |||||||||
Falsche Aussage. Punkt C liegt daher nicht auf der Geraden durch A und B. Damit liegen die drei Punkte nicht auf einer Geraden.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
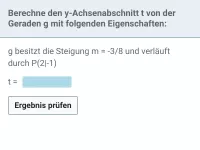
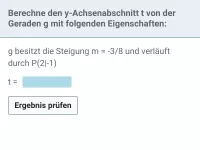
- Wie berechnet man den y-Achsenabschnitt einer Geraden, wenn die Steigung und ein Punkt bekannt sind?
- Wie berechnet man die Steigung einer Geraden mit zwei gegebenen Punkten?
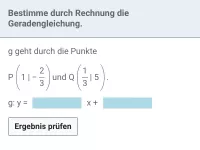
- Wie bestimmt man die Gleichung einer Geraden aus zwei gegebenen Punkten?
- Welche vier Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
- Wie bestimmt man die Steigung einer Geraden mit bekanntem y-Achsenabschnitt und einem weiteren Punkt?