Wie werden senkrechte und waagrechte Geraden in der Mathematik beschrieben?

Eine Besonderheit bilden waagrechte und senkrechte Geraden.

senkrechte Gerade werden durch die Gleichung "x = c" beschrieben
waagrechte Gerade werden durch die Gleichung "y = c" beschrieben.

Beachte, dass die Gleichung der senkrechten Gerade keine Funktionsgleichung ist und somit weder ein y-Achsenabschnitt noch eine Steigung angegeben werden kann. Das ist schon daran erkennbar, dass hier Punkte des Graphen "übereinander" liegen, was bei einer Funktion nicht vorkommen darf.

Beispiel 1

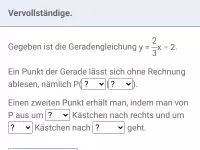
Gib für die eingezeichneten Geraden sowie für die x-und y-Achse eine Geradengleichung an:

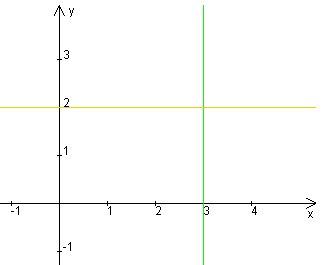
Lösung:

Für die orange Gerade gilt m = 0 und t = 2 und damit die Gleichung y = 2.
Für die x-Achse gilt m = 0 und t = 0 und damit die Gleichung y = 0.
Für die grüne Gerade kann weder m noch t sinnvoll angegeben werden. Ihre Gleichung lautet x = 3.
Die y-Achse wird demnach durch die Gleichung x = 0 beschrieben.

Lernvideo

Lineare Funktion, senkrechte und waagrechte Geraden

Kanal: Mathegym

Beispiel 2

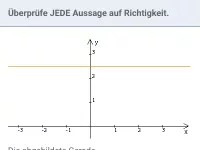
Gib für die eingezeichneten Geraden sowie für die x-und y-Achse eine Geradengleichung an:

Lösung:

Für die orange Gerade gilt m = 0 und c = 2 und damit die Gleichung y = 2.
Für die x-Achse gilt m = 0 und c = 0 und damit die Gleichung y = 0.
Für die grüne Gerade kann weder m noch c sinnvoll angegeben werden. Ihre Gleichung lautet x = 3.
Die y-Achse wird demnach durch die Gleichung x = 0 beschrieben.

Beispiel 3

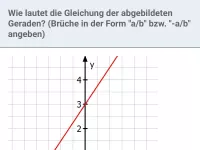
Gib für die eingezeichneten Geraden sowie für die x-und y-Achse eine Geradengleichung an:

Lösung:

Für die orange Gerade gilt m = 0 und n = 2 und damit die Gleichung y = 2.
Für die x-Achse gilt m = 0 und n = 0 und damit die Gleichung y = 0.
Für die grüne Gerade kann weder m noch n sinnvoll angegeben werden. Ihre Gleichung lautet x = 3.
Die y-Achse wird demnach durch die Gleichung x = 0 beschrieben.

Siehe auch