Wie zeichnet man eine Gerade, wenn Steigung m und y-Achsenabschnitt t bekannt sind?
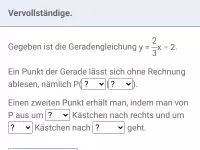
Um die Gerade mit der Gleichung y=mx+t zu zeichnen, gehe am besten wie folgt vor:
- Stelle die Steigung m als Bruch dar (falls nicht schon als Bruch gegeben), z.B. m = -1/4 .
- Gehe vom Schnittpunkt mit der y-Achse, also P(0|t) aus um den Nennerbetrag, hier also um 4, nach rechts.
- Gehe dann um den Zählerbetrag nach oben (falls m postiv) bzw. unten (falls m negativ). Hier also um 1 nach unten. Damit hast du einen zweiten Punkt und kannst die Gerade zeichnen.
Beispiel 1
Zeichne die Gerade mit folgender Gleichung:
y | = |
|
Lösung:
y | = |
|
m | = |
|
t | = | 2 |
Für die Zeichnung werden zwei Punkte benötigt:
- Der erste ergibt sich aus t, also (0|2)
- geht man von dort aus gemäß der Steigung m um 1 Einheit nach unten (Zähler negativ, darum nach unten) und 3 Einheiten nach rechts, so erhält man den zweiten Punkt
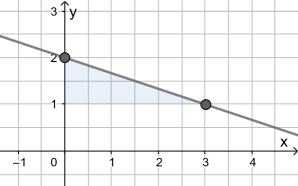
Statt Längeneinheiten könnte man auch Kästchen abgehen (1 Kästchen nach unten und 3 nach rechts). Das Steigungsdreieck fällt dabei natürlich kleiner aus, aber die Gerade ist dieselbe:
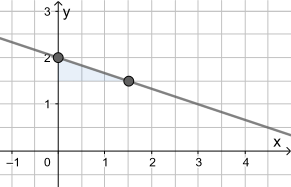
Beispiel 2
Bestimme zeichnerisch: Welchen y-Achsenabschnitt besitzt die Gerade g, die durch den Punkt (−3|−1) geht und parallel ist zur Geraden h mit der Gleichung
y | = |
|
Wenn g und h parallel sind, muss g dieselbe Steigung wie h haben. Die Steigung von h kann man aus der gegebenen Gleichung
(umgestellt) ablesen. Es gilt somit
h: y | = |
|
| = |
|
Um einen zweiten Punkt der Geraden g zu erhalten, geht man also vom Punkt (−3|−1) aus um 1 Einheit nach unten und um 4 Einheiten nach rechts. Die Gerade g schneidet die y-Achse dann in (0|-1,75), d.h.
| . |
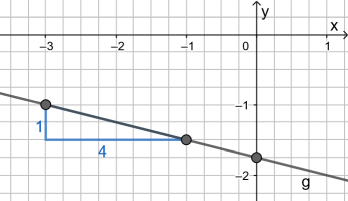
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was ist die allgemeine Gleichung einer linearen Funktion und was bedeuten die Parameter m und t?
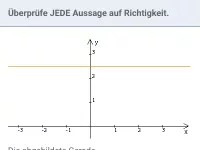
- Wie werden senkrechte und waagrechte Geraden in der Mathematik beschrieben?
- Wie löst man eine lineare Gleichung zeichnerisch?
- Wie kann eine lineare Gleichung mit zwei Variablen interpretiert werden?
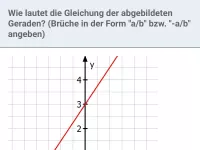
- Wie bestimmt man den Funktionsterm einer grafisch dargestellten Geraden?
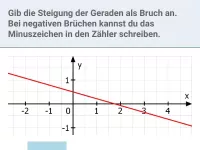
- Wie bestimmt man die Steigung einer Geraden und was sagt sie aus?