Wie bestimmt man den Funktionsterm einer grafisch dargestellten Geraden?

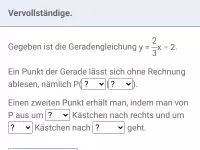
Um den Funktionsterm einer abgebildeten Geraden aufzustellen, musst du ihren y-Achsenabschnitt und ihre Steigung ermitteln:
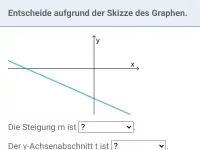
  1. Der y-Achsenabschnitt lässt sich direkt aus dem Schnittpunkt der Geraden mit der y-Achse ablesen.
  2. Die Steigung erhältst du so: suche zwei Punkte auf der Geraden, deren Koordinaten sich gut ablesen lassen und betrachte das Steigungsdreieck zwischen diesen beiden Punkten. Bilde den Bruch aus der Höhe des Dreiecks im Zähler und der Breite des Dreiecks im Nenner und kürze diesen, falls möglich. Falls die Gerade fällt, schreibe noch ein Minus vor den oben ermittelten Bruch. Damit hast du die Steigung.
Beispiel 1
Lies jeweils die genauen Werte für m und t ab:
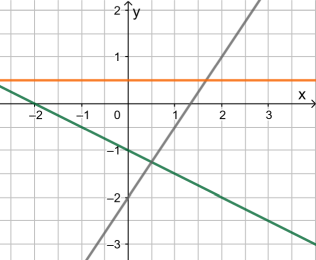
graphik
  • Schwarz:
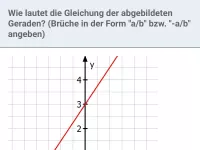
Die Gerade schneidet die y-Achse im Punkt (0|-2), also 
t
=
−
2
. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|1) ab und betrachtet dann das sogenannte Steigungsdreieck zwischen diesen Punkten:
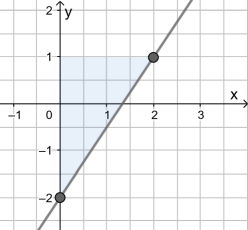
graphik
Das Dreieck ist 3 Kästchen hoch und 2 Kästchen breit, also lautet die (positive!) Steigung 
m
=
+
3
2
.
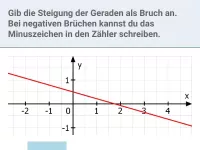
  • Grün:
Die Gerade schneidet die y-Achse im Punkt (0|-1), also 
t
=
−
1
. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|-2) ab und betrachtet dann das Steigungsdreieck:
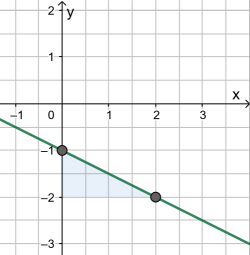
graphik
Das Dreieck ist 1 Kästchen hoch und 2 Kästchen breit, also lautet die (negative!) Steigung 
m
=
−
1
2
.
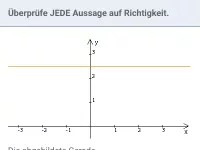
  • Orange:
Die Gerade schneidet die y-Achse im Punkt (0|0,5), also 
t
=
0,5
 und ist parallel zur x-Achse, also 
m
=
0
.
Lineare Funktion, Bestimmung des Funktionsterms anhand der Geraden, Beispiele
Lernvideo

Lineare Funktion, Bestimmung des Funktionsterms anhand der Geraden, Beispiele

Kanal: Mathegym
Beispiel 2
Lies jeweils die genauen Werte für m und b ab:
graphik
Lösung:
  • Schwarz:
Die Gerade schneidet die y-Achse im Punkt (0|−2), also b = −2. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|1) ab und betrachtet dann das sogenannte Steigungsdreieck zwischen diesen Punkten:
graphik
Das Dreieck ist 3 Kästchen hoch und 2 Kästchen breit, also lautet die (positive!) Steigung m = +3/2.
  • Grün:
Die Gerade schneidet die y-Achse im Punkt (0|−1), also b = −1. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|−2) ab und betrachtet dann das Steigungsdreieck:
graphik
Das Dreieck ist 1 Kästchen hoch und 2 Kästchen breit, also lautet die (negative!) Steigung m = −1/2.
  • Orange:
Die Gerade schneidet die y-Achse im Punkt (0|0,5), also b = 0,5 und ist parallel zur x-Achse, also m = 0.
Beispiel 3
Lies jeweils die genauen Werte für m und c ab:
graphik
Lösung:
  • Schwarz:
Die Gerade schneidet die y-Achse im Punkt (0|-2), also c = -2. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|1) ab und betrachtet dann das sogenannte Steigungsdreieck zwischen diesen Punkten:
graphik
Das Dreieck ist 3 Kästchen hoch und 2 Kästchen breit, also lautet die (positive!) Steigung m = +3/2.
  • Grün:
Die Gerade schneidet die y-Achse im Punkt (0|-1), also c = -1. Um m zu ermitteln, liest man einen zweiten Punkt, z.B. (2|-2) ab und betrachtet dann das Steigungsdreieck:
graphik
Das Dreieck ist 1 Kästchen hoch und 2 Kästchen breit, also lautet die (negative!) Steigung m = -1/2.
  • Orange:
Die Gerade schneidet die y-Achse im Punkt (0|0,5), also c = 0,5 und ist parallel zur x-Achse, also m = 0.)
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen