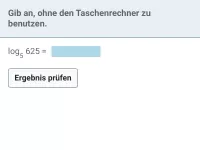
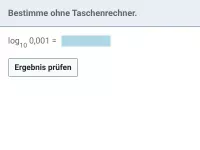
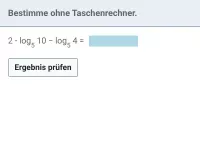
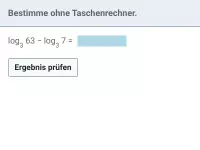
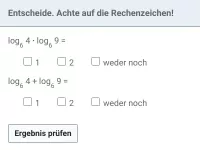
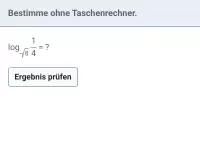
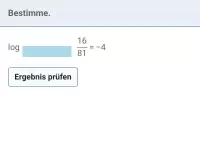
Wie kann man log_b(a) ohne Taschenrechner bestimmen, wenn Basis und Argument als Potenzen derselben Basis darstellbar sind?
Lassen sich Basis und Argument des Logarithmus als Potenz derselben Basis schreiben, so kann man den Logrithmuswert ohne Taschenrechner bestimmen.
Beispiel
| = | ? |
Die zum Logarithmus passende Gleichung lautet:
| = |
|
Sowohl 4 als auch
lassen sich als Potenz mit Basis 2 schreiben:
1 |
8 |
4 | = |
|
| = |
|
Eingesetzt in die Gleichung von oben:
| = |
| links Potenzgesetz anwenden | |||||||||||||
| = |
| Exponenten gleichsetzen (da Basis gleich) | |||||||||||||
| = |
| ||||||||||||||
| = |
| ||||||||||||||
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was bedeutet log_b a und wie berechnet man es?
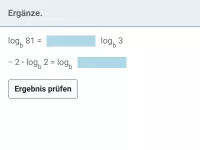
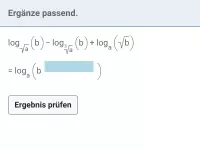
- Wie lassen sich mehrere Logarithmen mit gleicher Basis zu einem Logarithmus zusammenfassen?
- Wie kann man einen Logarithmus umformen, wenn das Argument eine Potenz ist?
- Wie berechnet man log_b a mit einem Taschenrechner, der nur eine 'log'-Taste hat?
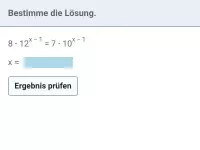
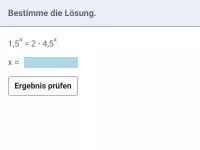
- Was ist eine Exponentialgleichung und wie wird sie gelöst?
- Wie lässt sich eine Exponentialgleichung der Form b^{T_1(x)} = b^{T_2(x)} lösen?
- Wie löst man die Gleichung log_b a = c, wenn a oder b gesucht sind?
- Wie kann ein Logarithmus umgeformt werden, wenn die Basis eine Potenz ist?
- Wie löst man eine Exponentialgleichung, wenn nur eine Potenz mit x vorkommt?
- Wie kann man Summen oder Differenzen von Potenzen mit x im Exponenten vereinfachen?