Wie löst man eine Exponentialgleichung, wenn nur eine Potenz mit x vorkommt?

Exponentialgleichungen, in denen nur eine Potenz (und sonst kein weiteres x) vorkommt, lassen sich in die Form

aT(x)=b

bringen [mit T(x) ist ein x-Term wie z.B. x+3 gemeint]. Sofern b>0, kann man anschließend auf beiden Seiten den Logarithmus zur Basis a anwenden, womit man die Gleichung

T(x)=logab

erhält, die nach x aufgelöst werden kann.
Beispiel
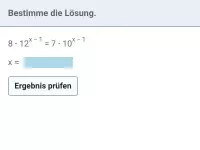
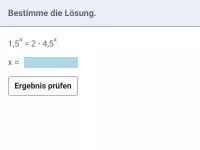
Löse die Gleichung.
12 000
·
1,06
x
−
3
=
10
5
12 000
·
1,06
x
−
3
=
10
5
:
12 000
1,06
x
−
3
=
10
5
12 000
log
1,06
x
−
3
=
log
1,06
10
5
12 000
+
3
x
=
log
1,06
10
5
12 000
+
3
 
≈
 
39,3876
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen