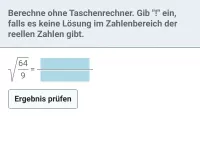
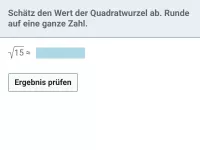
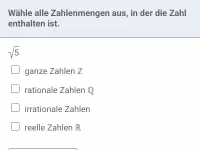
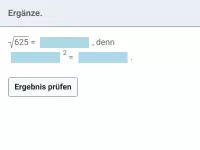
Was ist die Definition von \( \sqrt{a} \), was ist der Radikand und welche Bedingungen muss dieser erfüllen?

Die Wurzel einer nicht negativen Zahl a ist diejenige nicht negative Zahl Zahl, die quadriert a ergibt, also

(√a)2 = a.

Die Zahl unter der Wurzel nennt man Radikand.

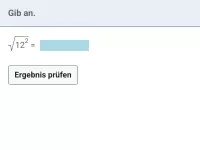
Laut dieser Definition gilt also: Weder der Radikand noch der Wert des Wurzelterms dürfen/können negativ sein!
Beispiel 1
0,0016
=
16
10000
=
4
100
2
=
4
100
=
0,04
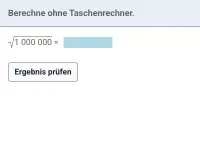
Beispiel 2
3
6
25
=
81
25
=
9
5
2
=
9
5
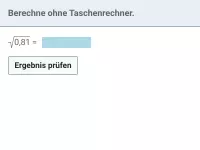
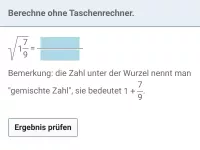
Beispiel 3
16
=
▇
, denn 
▇
2
=
▇
.
16
=
4
, denn 
4
2
=
16
.
Die Zahl 
16
 ist eine Zahl (x) die mit sich selbst malgenommen 
x
·
x
=
x
2
 die Zahl unter dem Wurzelzeichen (16) ergibt. Die gesuchte Zahl x ist hier 4, denn 
4
·
4
=
4
2
=
16
.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen