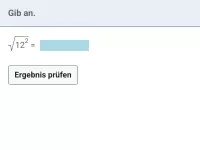
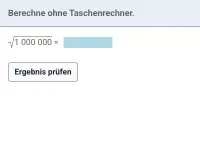
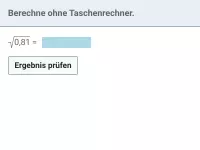
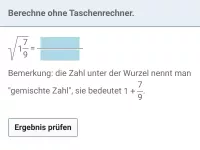
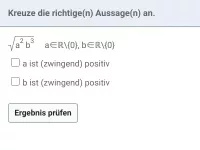
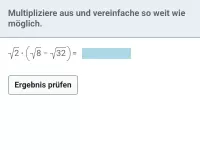
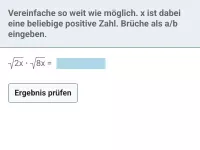
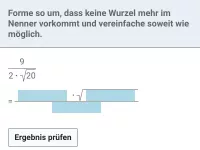
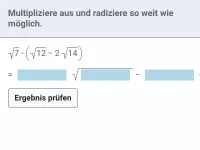
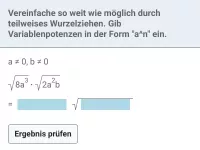
Wie kann man \( \sqrt{a^2} \) vereinfachen, wenn a auch negativ sein könnte?

Beachte beim Rechnen mit Variablen, dass (weil a auch negativ sein könnte)

√(a²) = | a |

Der Betragstrich ist nicht nötig, wenn a < 0 ausgeschlossen werden kann. Ist hingegen bekannt, dass a negativ ist, kann man statt des Betrags auch konkret schreiben

√(a²) = −a

Ob eine Variable unter der Wurzel positiv oder negativ ist, erschließt sich oft indirekt aus der Aufgabenstellung.

Beispiel 1
Gegeben ist der Term 
x
6
.
Welche Werte können für x eingesetzt werden und wie lautet der vereinfachte Term?
Lösung:
Wichtig ist, dass der Radikand (Term unter der Wurzel) nicht negativ ist. Das wird allein schon durch den geradzahligen Exponenten verhindert, weshalb es für x keinerlei Einschränkungen gibt.
Die Rechnung 
x
6
=
x
3
 ist falsch, da x auch negativ sein könnte und in diesem Fall 
x
3
, also der Wert der Wurzel, ebenfalls negativ wäre - was nicht sein darf! Darum ist es wichtig, einen Betrag um 
x
3
 zu setzen:
x
6
=
x
3
Nur wenn man weiß, dass x positiv ist oder Null, kann man auf die Betragstriche verzichten. Falls x garantiert negativ ist, kann man 
x
3
 auch schreiben als 
−
x
3
.
Vorsicht beim Wurzelziehen mit Variablen
Lernvideo

Vorsicht beim Wurzelziehen mit Variablen

Kanal: Mathegym
Beispiel 2
Vereinfache (a > 0, b > 0):
a
2
+
ab
−
a
+
b
:
a
−
1
a
2
+
ab
−
a
+
b
:
a
−
1
=
a
2
+
ab
−
a
+
b
a
−
1
als Bruchterm
=
a
·
a
+
b
−
a
+
b
a
−
1
a ausgeklammert
=
a
·
a
+
b
−
a
+
b
a
−
1
Wurzel aufgeteilt
=
a
−
1
·
a
+
b
a
−
1
a
+
b
 
ausgeklammert
=
a
−
1
·
a
+
b
a
+
1
·
a
−
1
3. bin. Formel
=
a
+
b
a
+
1
gekürzt
Quadratwurzel, Binomische Formel, Beispiel
Lernvideo

Quadratwurzel, Binomische Formel, Beispiel

Kanal: Mathegym
Beispiel 3
Vereinfache (x ≠ 0)
3
 
−
4x
2
y
:
12y
4
Vorbemerkung: Der linke Wurzelterm ist nur für 
y
 
<
 
0
 definiert, da ansonsten der Radikand negativ wäre (das Quadrat von x ist positiv).
3
 
−
4x
2
y
:
12y
4
=
3
 
−
4x
2
 
y
12y
4
unter einer Wurzel
=
3
 
−
x
2
3y
3
gekürzt
=
3
 
x
y
 
−
1
3y
teilweise radiziert
=
3
 
x
−
y
 
−
1
3y
Betrag unten aufgelöst
=
−
3
 
x
y
 
−
1
3y
Erläuterung: der Betrag lässt sich auflösen, da man weiß, dass y negativ ist (siehe Vorbemerkung). Wenn man die Betragstriche um eine Variable, deren Wert garantiert negativ ist, entfernt, muss an deren Stelle ein Minuszeichen vor die Variable gesetzt werden. Das Minuszeichen bewirkt, ebenso wie die Betragstriche, dass sich ein positiver Wert ergibt.
 
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen