Wie funktioniert der Heron-Algorithmus zur Bestimmung von Quadratwurzeln?
Der Heron-Algorithmus ist ein Verfahren, mit dem sich √a, also die Wurzel von a für a∈Q+, mit zunehmender Genauigkeit bestimmen lässt.
- Man startet am besten mit einer Zahl x1, deren Quadrat in etwa a entspricht. Teilt man a durch diesen Startwert x1, so erhält man eine Zahl y1, die zusammen mit x1 das Intervall absteckt, in dem √a liegt.
- Man rechnet nun die Mitte dieses Intervalls aus, also ½·(x1+y1), und fährt mit diesem neuen Wert (= x2) in dem Algorithmus fort.
Beispiel
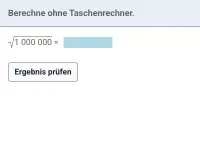
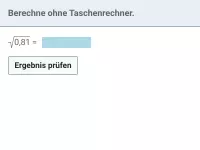
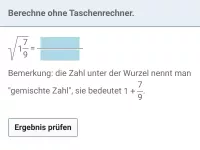
Bestimme
auf drei Dezimalstellen genau.
|
| 5 |
Lösung mit dem Heron-Algorithmus:
| − |
| = | 2 |
| = | 2,5 |
| [2 ; 2,5] |
| − |
| = | 2,25 |
| = |
|
|
|
| − |
| = |
|
| = | 2,2360… |
|
|
Damit ist die geforderte Genauigkeit gegeben, d.h.
.
| = | 2,236… |

Lernvideo
Der alte Grieche in deinem Taschenrechner - das Heron-Verfahren
Kanal: Mathegym
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
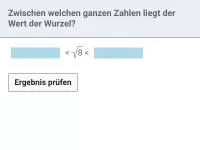
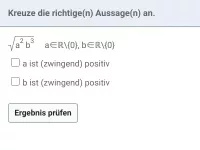
- Was ist die Definition von \( \sqrt{a} \), was ist der Radikand und welche Bedingungen muss dieser erfüllen?
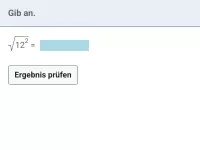
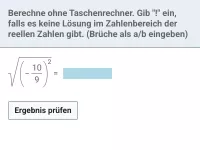
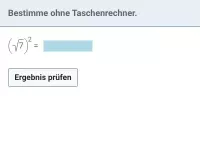
- Wie kann man \( \sqrt{a^2} \) vereinfachen, wenn a auch negativ sein könnte?
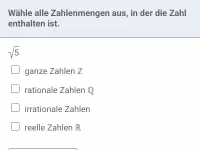
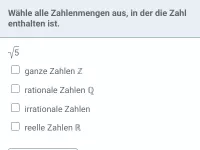
- Was sind die Zahlenmengen N, Z, Q und R und wie unterscheiden sie sich?
- Was bedeutet der Ausdruck a² in der Mathematik?
- Was sind reelle Zahlen und welche Zahlenarten gehören dazu?
- Wie kann man Wurzelausdrücke mit Minus-Vorzeichen berechnen?