Was sind die Zahlenmengen N, Z, Q und R und wie unterscheiden sie sich?
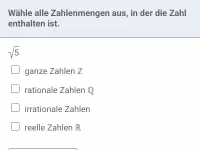
Unterscheide folgende Zahlenmengen:
- N = {1, 2, 3, ...}
Menge der natürliche Zahlen - Z = {0, ±1, ±2, ±3, ...}
Menge der ganze Zahlen; enthält über N hinaus auch noch 0 und die negativen (ganzen) Zahlen - Q = {p/q | p ∈ Z, q ∈ N}
Menge der rationalen Zahlen; enthält über Z hinaus auch noch alle (nicht ganzzahligen) Brüche - R
Menge der reellen Zahlen; enthält über Q hinaus auch noch alle irrationalen Zahlen wie z.B. √2 oder π
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈9. Klasse - Aufgaben + Stoff + Video
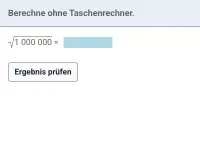
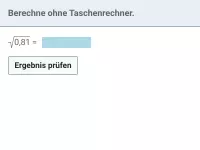
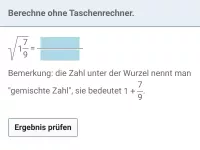
Quadratwurzeln - Einführung, Heron-Verfahren
Bestimmung einfacher Quadratwurzeln, Erkennen irrationaler Zahlen, annähernde Bestimmung mit dem Heron-Algorithmus, Vorzeichenbetrachtung bei Variablen unter der Wurzel -
≈9. Klasse - Aufgaben + Stoff
Rechnen mit reellen Zahlen - Zahlenmengen
Unterscheidung der Mengen ℕ, ℤ, ℚ und ℝ; Lösungen unterschiedlicher Gleichungstypen der jeweils passenden Menge zuordnen
Ähnliche Themen
- Was ist die Definition von \( \sqrt{a} \), was ist der Radikand und welche Bedingungen muss dieser erfüllen?
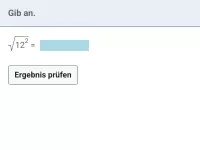
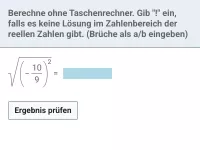
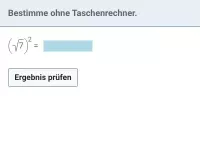
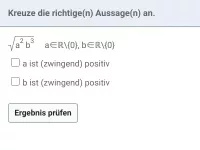
- Wie kann man \( \sqrt{a^2} \) vereinfachen, wenn a auch negativ sein könnte?
- Was bedeutet der Ausdruck a² in der Mathematik?
- Wie funktioniert der Heron-Algorithmus zur Bestimmung von Quadratwurzeln?
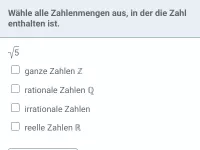
- Was sind reelle Zahlen und welche Zahlenarten gehören dazu?
- Wie kann man Wurzelausdrücke mit Minus-Vorzeichen berechnen?