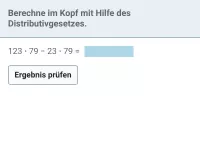
Was besagt das Distributivgesetz in der Mathematik?

Distributivgesetz:

a · (b + c ) = a · b + a · c    ("Klammer ausmultiplizieren")

(a + b ) : c = a : c + b : c

Statt + kann man auch − einsetzen, d.h. das Distributivgesetz gilt für Summen wie auch für Differenzen, die mit einer Zahl multipliziert oder durch eine Zahl dividiert werden.

Beispiel 1
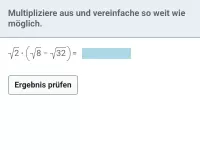
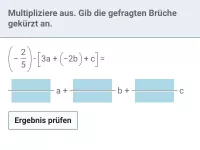
Multipliziere aus und gib gekürzt an:
−
1
3
·
−
2a
+
−
12b
+
3c
=
?
Lösung:
−
1
3
·
−
2a
2
3
 
a
+
−
1
3
·
−
12b
4b
+
−
1
3
·
3c
−
c
=
2
3
 
a
+
4b
−
c
Beispiel 2
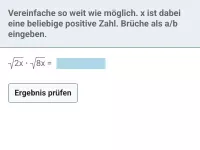
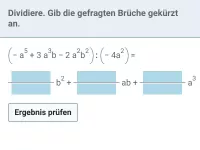
Multipliziere aus und gib gekürzt an:
5
3
 
ab
−
1
3
 
a
2
−
3b
·
−
6
5
=
?
- - - - - - - - - - - - - - - - - - Klammer in wertgleiche Summe umwandeln:
5
3
 
ab
+
−
1
3
 
a
2
+
−
3b
·
−
6
5
=
5
3
 
ab
·
−
6
5
−
2ab
+
−
1
3
 
a
2
·
−
6
5
2
5
 
a
2
+
−
3b
·
−
6
5
18
5
 
b
=
−
2ab
+
0,4a
2
+
3,6b
Beispiel 3
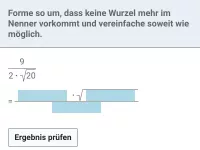
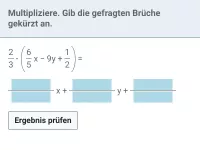
Multipliziere aus und gib gekürzt an:
2
9
·
3
5
−
6c
=
?
Lösung:
2
9
·
3
5
+
−
6c
=
2
9
·
3
5
2
15
+
2
9
·
−
6c
−
4
3
 
c
=
2
15
−
4
3
 
c
Beispiel 4
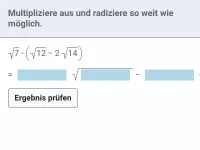
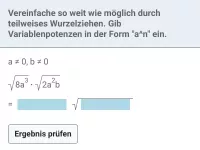
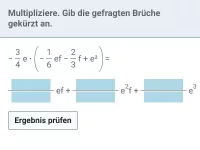
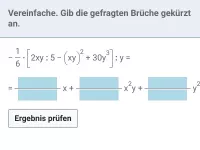
Vereinfache:
3
 
32
−
108
·
5
 
3
−
6
Lösung siehe Video:
Quadratwurzel, Termvereinfachung, Beispiel
Lernvideo

Quadratwurzel, Termvereinfachung, Beispiel

Kanal: Mathegym
Beispiel 5
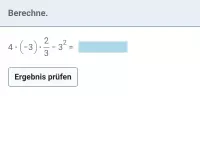
Löse durch Ausmultiplizieren:
6
·
40
+
7
=
?
·
40
+
6
·
?
=
?
+
?
=
?
Lösung:
6
·
40
+
7
=
6
·
40
+
6
·
7
=
240
+
42
=
282
Beispiel 6
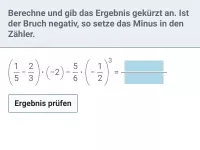
Zerlege geschickt und multipliziere aus:
9
·
37
=
9
·
30
+
?
geschickt zerlegt
=
?
·
30
+
9
·
?
ausmultipliziert
=
?
+
?
Punkt vor Strich
=
?
Endergebnis
9
·
37
=
9
·
30
+
7
geschickt zerlegt
=
9
·
30
+
9
·
7
ausmultipliziert
=
270
+
63
Punkt vor Strich
=
333
Endergebnis
Beispiel 7
3
·
3
−
27
=
?
 
 
 
3
·
3
−
27
=
3
·
3
−
3
·
27
=
3
·
3
−
3
·
27
=
9
−
81
=
3
−
9
=
−
6
Beispiel 8
Vereinfache:
12
+
20
−
2
 
27
·
5
36
12
+
20
−
2
 
27
·
5
36
=
4
·
3
+
4
·
5
−
2
 
9
·
3
·
1
36
·
5
teilweise radizieren
=
2
 
3
+
2
 
5
−
6
 
3
·
1
6
 
5
Klammer zusammenfassen
=
−
4
 
3
+
2
 
5
·
1
6
 
5
D-Gesetz
=
−
4
6
 
3
·
5
+
2
6
 
5
·
5
zusammenfassen
=
−
2
3
 
15
+
1
3
·
5
=
−
2
3
 
15
+
5
3
Ausführlicher im Video:
Quadratwurzeln - Verbindung der Grundrechenarten, D-Gesetz
Lernvideo

Quadratwurzeln - Verbindung der Grundrechenarten, D-Gesetz

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen