Sinusfunktion: welche Parameter wirken sich auf Amplitude und Periode aus? Präzisiere, bei welchen Werten es zu Streckung/Stauchung/Spiegelung an der y-Achse kommt.
Durch bestimmte Vorfaktoren lassen sich Amplitude und Periode der normalen Sinuskurve verändern. Amplitude beschreibt die Ausprägung in y-Richtung, normalerweise beträgt sie 1. Unter Periode versteht man die Länge des Intervalls, indem sich der Graph nicht wiederholt, normalerweise beträgt diese 2π. Gegenüber der normalen Sinuskurve (Kosinus analog) ist der Graph der Funktion
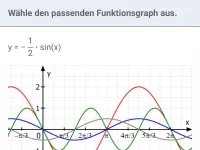
- y = a·sin(x) in y-Richtung gestreckt (|a| > 1) bzw. gestaucht (|a| < 1). Ist a negativ, erscheint der Graph zudem an der x-Achse gespiegelt.
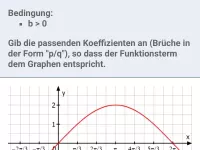
- y = sin(b·x), b>0, in x-Richtung gestreckt (0 < b < 1) bzw. gestaucht (b > 1). Ihre Periode ergibt sich aus 2π / b.
Beispiel
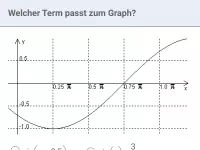
Der unten abgebildete Graph gehört zu einer Gleichung der Form
y | = |
|
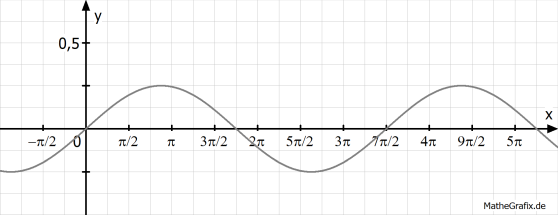
Bestimme a und b.
Die Amplitude (maximale Auslenkung nach oben gegenüber der Nullinie) beträgt 0,25, also
.
a | = |
|
Um b zu ermitteln, liest man zunächst die Periode ab; diese beträgt
. Durch einsetzen in die Formel
| π |
Periode | = |
|
und auflösen nach b erhält man:
| = |
|
| ||||||||||||||||||||
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Sinusfunktion: Welche Parameter führen zur Verschiebung in x- und in y-Richtung?
- Wie kommt man schrittweise von der normalen Sinuskurve zur Kurve mit der Gleichung y = a·sin[b·(x + c)] ; b>0 ?
- f(x) = a·sin(b·x); b>0 Gib Amplitude, Periode und Nullstellen an.
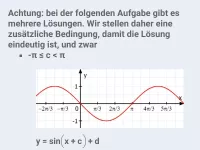
- Beschreibe, wie sich der Graph der Funktion y = a·sin(x + c) + d aus der normalen Sinuskurve ergibt.
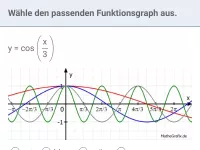
- Was lässt sich bzgl. des Graphen von y = sin(b·x) hinsichtlich Periode und Nullstellen sagen? Wie ist es bei y = cos(b·x) ?