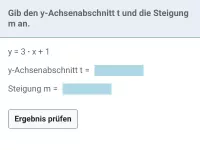
Was ist die allgemeine Gleichung einer Geraden und was bedeuten die darin vorkommenden Parameter?

Eine lineare Funktion mit der Gleichung y = m·x + b ergibt grafisch immer eine Gerade. Dabei ist m die Steigung (zeigt an, wie stark die Gerade steigt oder fällt) und b der y-Achsenabschnitt (zeigt an, wo die Gerade die y-Achse schneidet) der Gerade.
  • Ist m positiv, so steigt die Gerade (von links nach rechts)
  • Ist m negativ, so fällt die Gerade (von links nach rechts)
  • Ist m = 0, so verläuft die Gerade parallel zur x-Achse
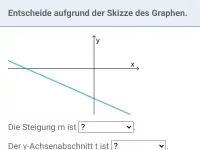
Beispiel 1
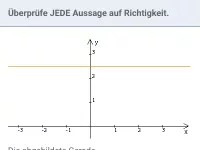
Welche Informationen lassen sich bzgl. der Steigung m und des y-Achsen-Abschnitts b ablesen?
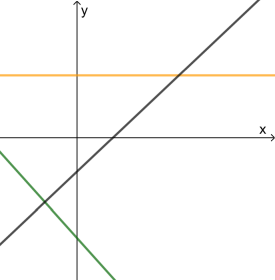
graphik
Lösung:
  • Schwarz: die Gerade steigt, d.h. m > 0 und schneidet die y-Achse im negativen Bereich, d.h. b < 0
  • Grün: die Gerade fällt, d.h. m < 0 und schneidet die y-Achse im negativen Bereich, d.h. b < 0
  • Orange: die Gerade ist parallel zur x-Achse, d.h. m = 0 und schneidet die y-Achse im positiven Bereich, d.h. b > 0
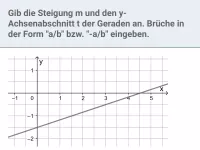
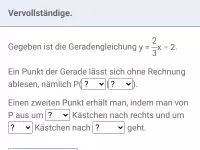
Beispiel 2
Zeichne die Gerade mit folgender Gleichung:
 
y
=
2
−
1
3
 
x
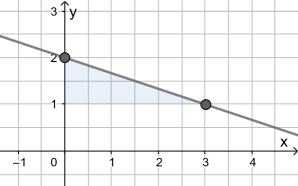
Lösung:
y
=
−
1
3
 
x
+
2
 
, also m
=
−
1
3
 
und b
=
2
Für die Zeichnung werden zwei Punkte benötigt.
  • Der erste ergibt sich aus b, also (0|2);
  • geht man von dort aus gemäß der Steigung m um 1 nach unten (Zähler negativ, darum nach unten) und 3 nach rechts, so erhält man den zweiten Punkt:
graphik
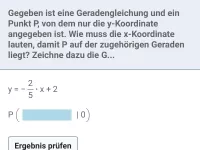
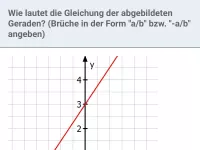
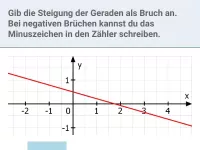
Beispiel 3
Bestimme zeichnerisch: Welchen y-Achsenabschnitt besitzt die Gerade g, die durch den Punkt (-3 ; -1) geht und parallel ist zur Geraden h mit der Gleichung y = 1 − 0,25x ?
Lösung siehe Video:
Lineare Funktion, Gerade gegeben durch Parallele und Punkt, Beispiel
Lernvideo

Lineare Funktion, Gerade gegeben durch Parallele und Punkt, Beispiel

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen