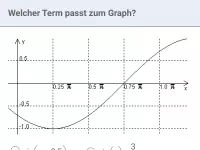
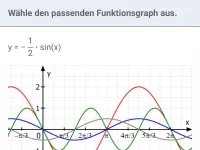
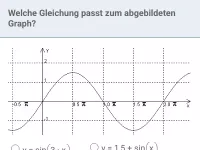
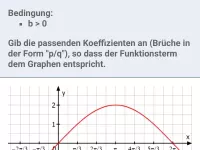
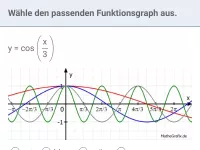
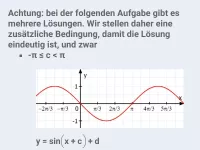
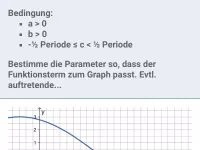
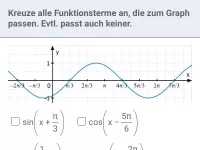
Wie bestimmt man Amplitude, Periode und Nullstellen der Funktion f(x) = a·sin(b·x) mit b>0?
Die Funktion f(x) = a·sin(b·x); b>0 bzw. deren Graph besitzt:
- die Amplitude |a|,
- die Periode 2π / b
- und damit folgende Nullstellen: außer 0 die halbe Periode und alle (positiven wie negativen) Vielfachen davon.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie beeinflussen Parameter die Amplitude und Periode der Sinusfunktion und wann kommt es zu Streckung, Stauchung oder Spiegelung?
- Wie beeinflussen die Parameter c und d die Verschiebung der Sinusfunktion in x- und y-Richtung?
- Wie transformiert man die Standard-Sinuskurve zur Funktion y = a·sin[b·(x + c)], b>0?
- Wie verändert sich die normale Sinuskurve zu y = a·sin(x + c) + d?
- Wie beeinflusst der Faktor b die Periode und Nullstellen der Funktionen y = sin(b·x) und y = cos(b·x)?