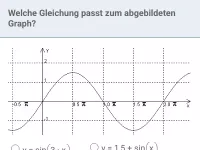
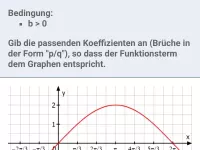
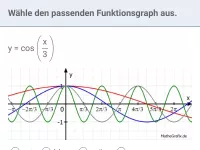
Wie beeinflusst der Faktor b die Periode und Nullstellen der Funktionen y = sin(b·x) und y = cos(b·x)?

Die Funktion f(x) = sin(b·x); b>0 bzw. deren Graph
  • ist gegenüber der normalen Sinuskurve in x-Richtung gestreckt (b<1) bzw. gestaucht (b>1).
  • besitzt die Periode 2π / b
  • und damit folgende Nullstellen: außer 0 die halbe Periode und alle (positiven wie negativen) Vielfachen davon.
Für den Kosinus gelten bzgl. Streckung/Stauchung und Periode dieselben Gesetzmäßigkeiten; das Rezept für die Nullstellen lautet hier: Nimm eine viertel Periode und addiere dazu (bzw. ziehe ab) eine halbe Periode (bzw. Vielfache davon).
Beispiel
Zeichne die Graphen zu folgenden Funktionen:
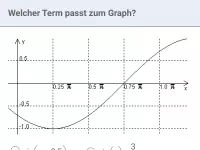
a) 
sin
 
2
3
·
x
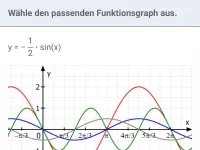
b) 
cos
 
3
2
·
x
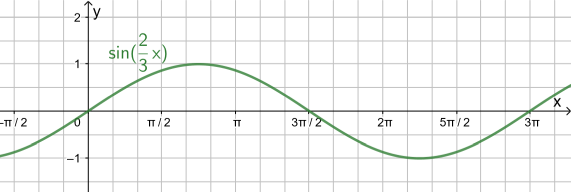
Lösung zu a)
Es liegt eine Streckung in x-Richtung vor, da x durch 
a
·
x
 mit 
a
 
<
 
1
 ersetzt wurde. Die Periode ergibt sich laut Formel durch 
2π
:
2
3
=
3π.
 Daraus wiederum ergeben sich Nullstellen bei 0; 1,5π; 3π usw.
graphik

Lösung zu b)
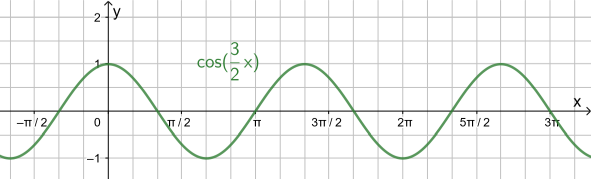
Es liegt eine Stauchung in x-Richtung vor, da x durch 
a
·
x
 mit 
a
 
>
 
1
 ersetzt wurde. Die Periode ergibt sich laut Formel durch 
2π
:
3
2
=
4
3
π.
 Daraus wiederum ergeben sich Nullstellen bei 
1
3
π;
 
π;
 
5
3
π;
 usw.
graphik
Sinuskurve, Streckung in x-Richtung
Lernvideo

Sinuskurve, Streckung in x-Richtung

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen