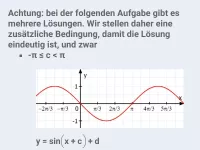
Wie transformiert man die Standard-Sinuskurve zur Funktion y = a·sin[b·(x + c)], b>0?

Der Graph der Funktion y = a·sin[b·(x + c)] ; b>0 entsteht aus der normalen Sinuskurve durch folgende Schritte:
  • Streckung/Stauchung in x-Richtung; die Periode ergibt sich durch 2π/b, vergößert sich also für b<1 und verkleinert sich für b>1
  • Verschiebung in x-Richtung um |c|; bei negativem Wert nach rechts, ansonsten nach links;
  • Streckung in y-Richtung mit dem Faktor |a|; zusätzlich Spiegelung an der x-Achse, wenn a negativ ist;
Für den Kosinus gelten die selben Gesetzmäßigkeiten.
Beispiel 1
f
 
x
=
cos
 
b
·
x
+
c
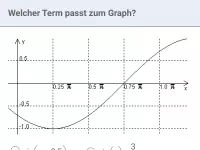
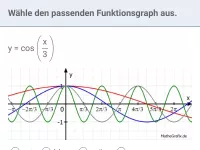
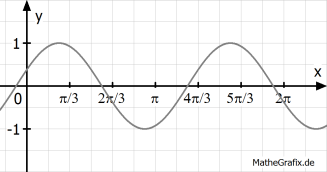
Bestimme passende Parameterwerte b und c 
b
 
>
 
0 und
−
π
 
<
 
c
 
<
 
π
, so dass der Funktionsterm zum abgebildeten Graphen passt.
graphik
Lösung:
Der Parameter b betrifft die Streckung/Stauchung in x-Richtung. Man berechnet b, indem man 2π durch die Periode teilt. Diese beträgt laut Graph 
4π
3
 (stell dir den Graphen um ein halbes Kästchen nach rechts verschoben vor, dann siehst du es deutlich) und damit 
b
=
2π
4π
3
=
1,5
.
Der Parameter c betrifft die Verschiebung in x-Richtung. Um wie viele Längeneinheiten muss also der der Graph von 
y
=
cos
 
1,5x
 noch nach rechts oder links verschoben werden, damit der abgebildete Graph entsteht? Antwort: z.B. um 1,5 Kästchen nach rechts, denn ohne Verschiebung liegt beim Kosinus für 
x
=
0
 ein Maximum vor, hier liegt ein Maximum 1,5 Kästchen rechts vom Ursprung vor.
"1,5 Kästchen" muss natürlich als π-Bruchteil angegeben werden. Dreisatz: 2 Kästchen entspricht 
π
3
, also entspricht ein halbes Kästchen 
π
12
, also entspricht 1,5 Kästchen 
3π
12
=
π
4
.
Eine Verschiebung um 
π
4
 nach rechts erzielt man, indem man x durch 
x
−
π
4
 ersetzt, also 
c
=
−
π
4
.
Beachte: sowohl für b als auch für c sind bei fehlender Einschränkung aufgrund der Symmetrie und Periodizität mehrere Lösungen möglich. Bei dieser Aufgabe ist aber 
b
 
>
 
0 und
−
π
 
<
 
c
 
<
 
π
 vorgegeben, damit ist die Lösung eindeutig.
sin(bx+c) und sin[b(x+c)]
Lernvideo

sin(bx+c) und sin[b(x+c)]

Kanal: Mathegym
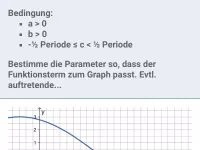
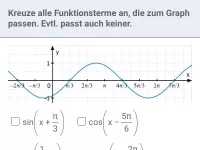
Beispiel 2
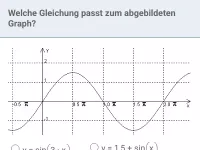
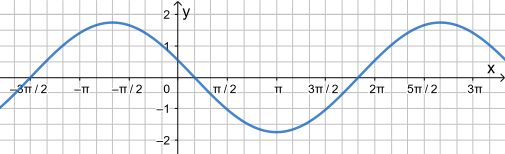
Welche der angegebenen Funktionsterme passen zum abgebildeten Graphen?
graphik
a
 
−
1,75
·
sin
 
0,6
·
x
−
π
6
b
 
1,75
·
sin
 
0,6
·
x
+
1,5π
c
 
1,5
·
sin
 
0,6
·
x
+
1,5π
    
    
d
 
1,75
·
sin
 
5
3
·
x
+
1,5π
e
 
1,75
·
sin
 
0,6
·
x
+
1,5π
+
1
f
 
1,75
·
sin
 
0,75
·
x
+
1,5π
  • Amplitude und Verschiebung in y-Richtung
Die y-Werte gehen von 
−
1,75
 bis 
1,75
, also beträgt die Amplitude 1,75. Damit scheidet (c) aus (hier ist die Amplitude 1,5). Da Minimum und Maximum vom Betrag her gleich sind gibt es keine Verschiebung in y-Richtung, weshalb (e) ausscheidet.

  • Periode
Wenn 6 Kästchen π entsprechen, dann entspricht ein Kästchen π/6. Von einer Nullstelle bis zur übernächsten (oder von einem Hochpunkt bis zum nächsten) zählen wir 20 Kästchen. Also beträgt die Periode 
20
·
π
6
=
10π
3
.
Der Faktor, der vor x im Argument steht ergibt sich laut Formel durch 
2π
:
Periode
, hier also 
2π
:
10π
3
=
2
·
3
10
=
0,6.
 Damit scheiden (d) und (f) aus.

  • Verschiebung in x-Richtung und Spiegelung an der x-Achse
Verschiebt man eine derart in y-Richtung und x-Richtung gestreckte Sinuskurve noch um 3π/2 nach links, so ergibt sich der abgebildete Graph. Daher ist (b) ein passender Term.
Alternativ könnte man die Sinuskurve aber auch an der y-Achse spiegeln (also −1,75) und dann um ein Kästchen, also π/6 nach rechts verschieben, um den abgebildeten Graph zu erhalten. Somit ist auch (a) ein passender Term.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen