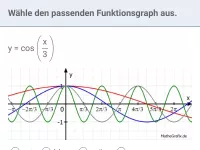
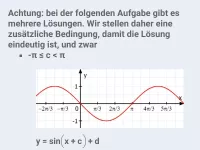
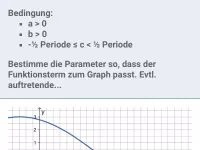
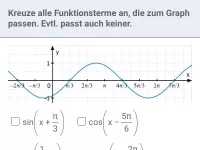
Wie beeinflussen die Parameter c und d die Verschiebung der Sinusfunktion in x- und y-Richtung?
Gegenüber der normalen Sinuskurve (Kosinus analog) ist der Graph der Funktion
- y = sin(x + c) in x-Richtung nach rechts (c < 0) bzw. links (c > 0) verschoben.
- y = sin(x) + d in y-Richtung nach oben (d > 0) bzw. unten (d < 0) verschoben.
Beispiel
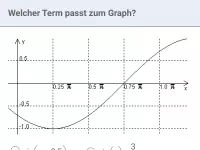
Gib die zum Graph passende Funktionsgleichung an:
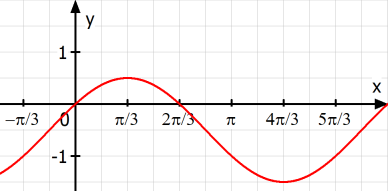
y | = |
|
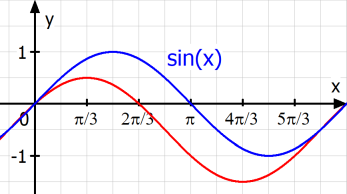
Lösung: man kann den Hochpunkt der gegebenen Kurve mit dem Hochpunkt der normalen Sinuskurve vergleichen. Wie man unten sieht, liegt der Hochpunkt der gesuchte Kurve ein Kästchen weiter links und ein Kästchen weiter unten. Da ein Kästchen in y-Richtung für 0,5 LE steht und in x-Richtung für
LE, entsteht der rote Graph also aus dem blauen durch Verschiebung um
nach links und um 0,5 nach unten. Ein passender Funktionsterm lautet demnach:
π |
6 |
π |
6 |
|

Lernvideo
Trigonometrie, Abwandlung der einfachen Sinusfunktion, Beispiel 1
Kanal: Mathegym
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie beeinflussen Parameter die Amplitude und Periode der Sinusfunktion und wann kommt es zu Streckung, Stauchung oder Spiegelung?
- Wie transformiert man die Standard-Sinuskurve zur Funktion y = a·sin[b·(x + c)], b>0?
- Wie bestimmt man Amplitude, Periode und Nullstellen der Funktion f(x) = a·sin(b·x) mit b>0?
- Wie verändert sich die normale Sinuskurve zu y = a·sin(x + c) + d?
- Wie beeinflusst der Faktor b die Periode und Nullstellen der Funktionen y = sin(b·x) und y = cos(b·x)?