Wie berechnet man den y-Achsenabschnitt einer Geraden, wenn die Steigung und ein Punkt bekannt sind?
Ist eine Gerade g durch ihre Steigung m und einen beliebigen Punkt P ∈ g gegeben, so kann man den y-Achsenabschnitt b leicht bestimmen:
- Ausgangspunkt ist die Geradengleichung y = m·x + b (für m setze die bekannte Steigung ein).
- Setze dann den Punkt P ein, d.h. ersetze x und y durch die Koordinaten von P.
- Löse schließlich die Gleichung nach dem gesuchten b auf.
Beispiel
Wo schneidet die Gerade, die durch
und P(2|−0,5) gegeben ist, die y-Achse?
m | = |
|
Lösung:
| = |
| setze die Koordinaten von P ein und löse dann nach b auf | ||||||||||||
| = |
| |||||||||||||
| = |
|
| ||||||||||||
| = |
| |||||||||||||
Also lautet der y-Achsenabschnitt
| . |

Lernvideo
Lineare Funktion aus einem Punkt und Steigung | Verständlich erklärt
Kanal: EZ-Mathe
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie berechnet man den y-Achsenabschnitt einer Geraden, wenn die Steigung und ein Punkt bekannt sind?
- Wie berechnet man die Steigung einer Geraden mit zwei gegebenen Punkten?
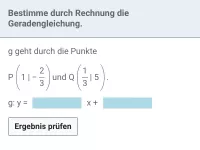
- Wie bestimmt man die Gleichung einer Geraden aus zwei gegebenen Punkten?
- Welche vier Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
- Wie bestimmt man die Steigung einer Geraden mit bekanntem y-Achsenabschnitt und einem weiteren Punkt?
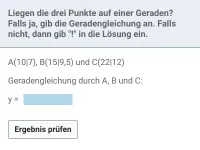
- Wie prüfst du rechnerisch, ob drei Punkte auf einer Geraden liegen?