Wie erkennt man exponentielles Wachstum anhand einer Wertetabelle?

Beim exponentiellen Wachstum ist der relative Zuwachs konstant, d.h.
  f(t+1) : f(t) = a (Wachstumsfaktor)

Bezogen auf eine Wertetabelle heißt das: der Quotient a = f(t+1) : f(t) benachbarter Funktionswerte ist konstant.

Unterscheide zwischen Wachstum (a > 1) und Abnahme (0 < a < 1)

Beispiel
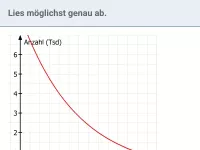
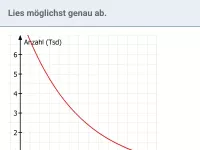
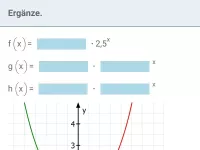
Ergänze so, dass es sich um exponentielles Wachstum handelt.
x
1
2
3
4
5
y
5
7
?
?
0,245
?
Da zwischen 
y
=
5
7
 und 
y
=
0,245
 drei Zeitschritte liegen, gilt für den Wachstumsfaktor a:
5
7
·
a
3
=
0,245
:
5
7
a
3
=
0,343
3
 
a
=
0,7
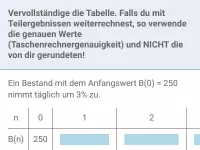
Berechne damit die fehlenden y-Werte:
5
7
·
0,7
=
0,5
    
x
=
2
0,5
·
0,7
=
0,35
    
x
=
3
0,245
·
0,7
=
0,1715
    
x
=
5
x
1
2
3
4
5
y
5
7
0,5
0,35
0,245
0,1715
Exponentielles Wachstum, Wachstumsfaktor, Beispiel 1
Lernvideo

Exponentielles Wachstum, Wachstumsfaktor, Beispiel 1

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen