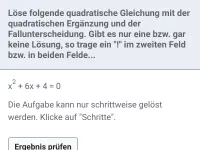
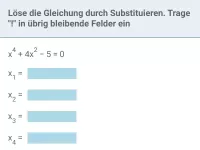
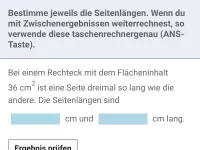
Wie funktioniert das Faktorisieren mit dem Rechteckmodell und wann wird es angewendet?

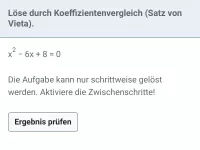
Faktorisieren mit dem Rechteckmodell (Satz von Vieta)

Beim Rechteck-Modell stellt man sich den quadratischen Term als Rechteck vor und sucht eine passende Unterteilung in vier Felder. Der Flächeninhalt des Gesamt-Rechtecks kann dann auf zwei Arten ermittelt werden:

Summe der Teilflächen (=Teilterme). Diese ergibt am Ende den gegebenen Gesamtterm.
"Länge mal Breite" des großen Rechtecks. Länge und Breite haben hierbei die Form ?x+?. Das Produkt der beiden Terme liefert damit die faktorisierte Form des gegebenen Terms.

Beispiel

Löse die quadratische Gleichung, indem du zunächst den quadratischen Term faktorisierst. Das Rechteck-Modell kann helfen.

10x

−

Der Koeffizient vor dem x²-Term ist 3, daher steht an den Seiten des Teil-Rechtecks oben links x und 3x (das Produkt bzw. der Flächeninhalt des Teil-Rechtecks liefert dann den korrekten x²-Term: x · 3x = 3x²).

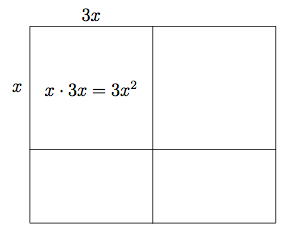
Der konstante Term -8 lässt sich zerlegen in 2 · (-4) bzw. (-2) · 4 oder 1 · (-8) bzw. (-1) · 8. Die einzelnen Paare werden als Seitenlängen eingetragen. Damit berechnest du die Flächeninhalte der Teil-Rechtecke, addierst alle zum Gesamt-Flächeninhalt auf und vergleichst mit dem gegebenen Term, um die korrekte Faktorisierung zu finden.

Achtung: Da das Rechteck oben links unterschiedliche Seitenlängen hat (x und 3x), macht es einen Unterschied, wie die beiden Faktoren, z.B. -4 und 2, im Rechteck eingetragen werden (siehe die beiden Beispiele in der oberen Reihe).

Aus der faktorisierten Gleichung lassen sich die Lösungen direkt ablesen. Denn ein Produkt ist gleich Null, genau dann, wenn einer der Faktoren gleich Null ist.