Was besagt der Satz von Vieta für quadratische Gleichungen?

Satz von Vieta: Die quadratische Gleichung in Normalform

x2 + px + q = 0

besitzt die beiden Lösungen x1 und x2, falls
  • x1 + x2 = −p und
  • x1·x2 = q
Beispiel
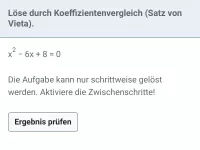
Löse mit Hilfe des Satzes von Vieta:
x
2
−
7x
+
6
=
0
Lösung: Suche zwei Zahlen, die multipliziert 6 und addiert +7 ergeben. Das trifft auf die Zahlen 1 und 6 zu. Also hat man zwei Lösungen der Gleichung gefunden:
x
1
=
1
x
2
=
6
Ausführlicher erläutert (einschließlich Beweis) in folgendem Video:
Satz von Vieta, Anwendung und Beweis
Lernvideo

Satz von Vieta, Anwendung und Beweis

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen