Wie kann man Polynome vom Grad 3 oder höher faktorisieren?

Polynome (d.h. ganzrationale Terme) vom Grad 3 oder höher lassen sich evtl. faktorisieren (also in ein Produkt aus mehreren Faktoren zerlegen), indem man

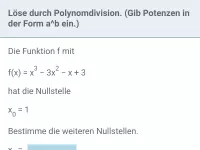
eine Nullstelle a errät und dann mittels Polynomdivision durch (x − a) teilt.
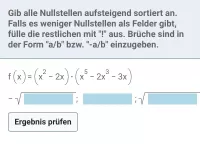
x oder eine höhere Potenz von x (z.B. x³) ausklammert. Das ist aber nur sinnvoll, wenn das Polynom keine additive Konstante aufweist, wie z.B. bei x³ - 4x² + 3x.
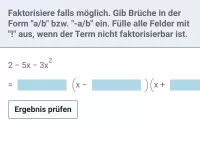
eine binomische Formel anwendet.

Ein quadratischer Faktor kann mit Hilfe der Mitternachtsformel evtl. weiter zerlegt werden. Eine ganzrationale Funktion vom Grad n hat höchstens n Nullstellen und zerfällt damit in höchstens n lineare Faktoren.

Siehe auch