Wie bestimmt man die Gleichung einer Geraden aus zwei gegebenen Punkten?
Ist eine Gerade durch zwei Punkte gegeben, so geht man wie folgt vor, um ihre Gleichung, sprich m und b, zu ermitteln:
- Bestimme zunächst die Steigung m = Δy / Δx .
- Setze dann in die Gleichung y = m·x + b die Koordinaten von einem der beiden Punkte ein und löse die Gleichung nach b auf.
Beispiel
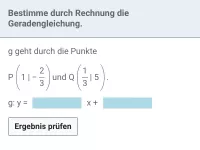
Ermittle die Gleichung der Geraden g, die durch die Punkte P1(−3|2) und P2(5|−4) geht.
- Ermittlung von m
| = |
|
| = | 8 |
| = |
|
- Ermittlung von b
Setze
sowie einen der beiden Punkt, z.B.
in die allgemeine Geradengleichung
ein und löse nach b auf.
m | = |
|
P | 1 |
y | = |
|
| = |
| m einsetzen | |||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
Die Gleichung der Geraden g lautet damit
.
|
Lernvideo
Id: 9LMRBuak6X8
Video-URL konnte nicht geladen werden.

Lernvideo
LINEARE FUNKTION Funktionsgleichung bestimmen – lineare Funktionen aufstellen
Kanal: MathemaTrick
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
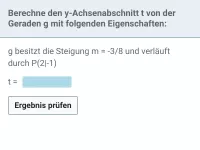
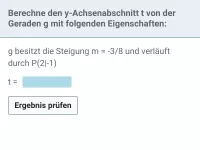
- Wie berechnet man den y-Achsenabschnitt einer Geraden, wenn die Steigung und ein Punkt bekannt sind?
- Wie berechnet man die Steigung einer Geraden mit zwei gegebenen Punkten?
- Wie bestimmt man die Gleichung einer Geraden aus zwei gegebenen Punkten?
- Welche vier Ausnahmefälle sind zu beachten, wenn man die Lage zweier Geraden zueinander untersucht?
- Wie bestimmt man die Steigung einer Geraden mit bekanntem y-Achsenabschnitt und einem weiteren Punkt?
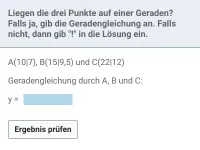
- Wie prüfst du rechnerisch, ob drei Punkte auf einer Geraden liegen?