Was ist das kleinste gemeinsame Vielfache (kgV) und wie wird es berechnet?
Unter dem kleinsten gemeinsamen Vielfachen (kgV) zweier natürlicher Zahlen a und b versteht man die kleinste natürliche Zahl, die sowohl ein Vielfaches von a als auch ein Vielfaches von b ist.
Einfaches Beispiel: die Zahlen 4 und 6 haben 12, 24, 36 usw. als gemeinsame Vielfache. Von diesen ist 12 die kleinste, also ist 12 das kgV von 4 und 6.
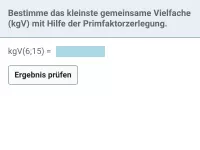
Das kgV kann mit unterschiedlichen Methoden bestimmt werden. Bei einfachen Zahlen kommt man oft schnell drauf, indem man von beiden Zahlen die ersten Vielfachen bildet und vergleicht. Ansonsten steht auch die Methode der Primfaktorenzerlegung zur Verfügung.
Beispiel 1
kgV(72; 104) | = | ? |
Lösung:
- 1. Schritt: Primfaktorzerlegung
72 | = |
|
104 | = |
|
- 2. Schritt: kgV ablesen
Das kgV ergibt sich immer aus ALLEN Faktoren der ersten Zeile (also der ersten Zahl, hier 72) sowie den Faktoren der zweiten Zeile, die darin noch nicht erfasst sind:
| = |
|
Beispiel 2
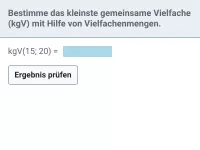
kgV(12; 15)=?
Betrachte die ersten Vielfachen beider Zahlen:
V(12) | = | {12; 24; 36; 48; 60; …} |
V(15) | = | {15; 30; 45; 60; …} |
Wie man sieht, ist 60 die erste Übereinstimmung zwischen beiden Vielfachenmengen und damit das kgV beider Zahlen.
Bemerkung: natürlich kannst du bei dieser Methode noch praktischer Vorgehen. Am einfachsten ist es, wenn man nur von der größeren beider Zahlen nacheinander die Vielfachen bildet und jedes mal überprüft, ob die andere Zahl ein Teiler davon ist. Im Beispiel oben ist 60 das erste Vielfache von 15, das auch durch 12 teilbar ist. Sobald das der Fall ist, hat man das kgV gefunden.
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈6. Klasse - Aufgaben + Stoff + Video
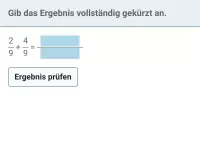
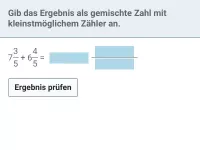
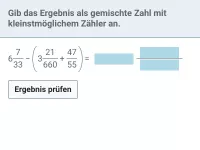
Brüche - Addition und Subtraktion - nur positiv
Addition und Subtraktion von Brüchen und gemischten Zahlen, komplexere Summen und Differenzen; Hauptnenner bzw. kgV ermitteln -
≈5. Klasse - Aufgaben + Stoff
Teilbarkeit - Teilermenge und Vielfachenmenge
kgV und ggT bestimmen können
Ähnliche Themen
- Wie kann jede ganze Zahl als Bruch dargestellt werden?
- Wie addiert man Brüche mit gleichem Nenner?
- Was muss man beachten, wenn man Brüche addiert oder subtrahiert?
- Wie addiert und subtrahiert man gemischte Zahlen?
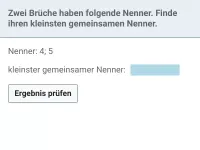
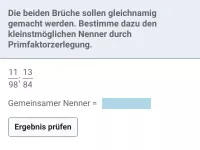
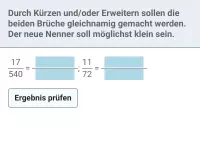
- Wie findet man den kleinsten gemeinsamen Nenner zweier Brüche?
- Wie subtrahiert man gemischte Zahlen, wenn der abzuziehende Bruch größer ist als der Bruch im Minuend?
- Wie findet man die Erweiterungsfaktoren für Brüche nach Bestimmung des kleinsten gemeinsamen Nenners?
- Was ist der ggT zweier natürlicher Zahlen und wie wird er ermittelt?
- Wie kann man das kleinste gemeinsame Vielfache (kgV) schnell bestimmen?