Was ist die Mitternachtsformel und wie bestimmt man die Anzahl der Lösungen?
Die Lösungen der quadratische Gleichung ax² + bx + c = 0 könnnen, falls vorhanden, immer mit der sog. Mitternachtsformel (MNF) bestimmt werden. Zunächst berechnet man die sog. Diskriminante:
D = b² − 4ac
Je nachdem, ob D positiv, null oder negativ ist, gibt es genau zwei, genau eine oder gar keine Lösung. Abgesehen vom letzten Fall heißt/heißen die Lösung(en):
x1,2 = (−b ± √D) : 2a
Beispiel 1
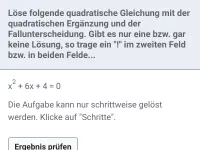
Löse die Gleichung:
| = |
|
- In die Nullform bringen (... = 0) und vereinfachen
| = |
|
| |||||||||||||||||||||||||||
| = |
| Umstellen (x² vorne, Konstante am Schluss) | |||||||||||||||||||||||||||
| = |
|
| |||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||
- Diskriminante berechnen
| ; |
|
| = | 76 |
- Lösungen besimmen
Da D > 0, gibt es zwei Lösungen:
| = |
|
| = |
|
| = |
|
Beispiel 2
Löse die Gleichung
.
| = | 0 |
Die Gleichung liegt bereits in der allgemeinen Form
vor (d.h. rechts vom "=" steht die Null und links vom "=" steht am Anfang
, dahinter …x und dahinter die Konstante).
| = | 0 |
…x | 2 |
- a, b und c ablesen
a | = | 2 |
x | 2 |
b | = |
|
x
c | = |
|
Beachte: das Rechenzeichen vor den Zahlen ist (als Vorzeichen gedacht) jeweils mitzunehmen!
- Diskriminante D bestimmen
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
D > 0 und damit gibt es zwei Lösungen:
- Lösungen mit MNF bestimmen
| = |
| ||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||
| = |
|
| = |
|
Die MNF wird auch im folgendem Video genau erklärt:

Lernvideo
Mitternachtsformel (MNF), Beispielaufgaben
Kanal: Mathegym
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie macht man eine Bruchgleichung nennerfrei und was sollte man beachten?
- Welche zwei Spezialfälle quadratischer Gleichungen ermöglichen eine Lösung ohne die allgemeine Lösungsformel und wie löst man diese?
- Was sind die rückwärts gerichteten binomischen Formeln und wie werden sie angewendet?
- Wie kann eine quadratische Gleichung eine oder zwei Lösungen haben? Gib jeweils ein Beispiel und begründe dies.
- Was besagt der Satz von Vieta für quadratische Gleichungen?
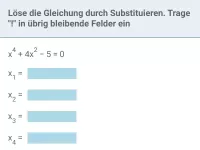
- Wie funktioniert die Substitutionsmethode in der Mathematik?
- Was ist die pq-Formel und wofür wird sie verwendet?
- Wie wendet man die pq-Formel auf eine quadratische Gleichung der Form ax² + bx + c = 0 mit a ≠ 1 an?
- Wie funktioniert das Faktorisieren mit dem Rechteckmodell und wann wird es angewendet?
- Was ist bei einer quadratischen Gleichung mit einem Parameter zu beachten?