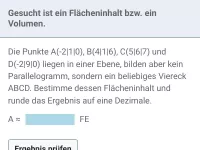
Wie bestimmt man den Schnittwinkel zwischen zwei Geraden, einer Geraden und einer Ebene sowie zwischen zwei Ebenen?

Für den Winkel \( \alpha \) zwischen zwei Vektoren (stelle sie dir in ihren Fußpunkten zusammengelegt vor, \( 0^\circ \le \alpha \le 180^\circ \)) gilt:

\[ \cos(\alpha) = \frac{\text{Skalarprodukt beider Vektoren}} {\text{Produkt ihrer Längen}} \]

Den Winkel zwischen anderen geometrischen Objekten bestimmt man wie folgt:

  • Sich schneidende Geraden \( g \) und \( h \): Bestimme den Winkel zwischen den zugehörigen Richtungsvektoren (Ist dieser \( > 90^\circ \), subtrahiere ihn noch von \( 180^\circ \)).
  • Sich schneidende Gerade \( g \) und Ebene \( E \): Subtrahiere den Winkel zwischen dem Richtungsvektor von \( g \) und dem Normalenvektor von \( E \) von \( 90^\circ \) (und nimm den Betrag des Ergebnisses, falls nötig).
  • Sich schneidende Ebenen \( E \) und \( F \): Bestimme den Winkel zwischen den zugehörigen Normalenvektoren (Ist dieser \( > 90^\circ \), subtrahiere ihn noch von \( 180^\circ \)).
Beispiel
Berechne den Schnittwinkel zwischen den Ebenen \(E_1\) und \(E_2\text{:}\) \[ E_1: \; 2x + y - z - 3 = 0 \] \[ E_2: \; x - y + 2z - 1 = 0 \]

Der Schnittwinkel lässt sich berechnen als Winkel zwischen den beiden Normalenvektoren \(\vec{n_1}=\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}\) und \(\vec{n_2}=\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}\text{:}\) \[ \begin{aligned} cos\,\varphi &=\frac{\left\lvert \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}\circ\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} \right\rvert}{\left\lvert \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}\right\rvert\cdot \left\lvert \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} \right\rvert}\\[15pt] &= \frac{\lvert 2\cdot 1+1\cdot(-1)+(-1)\cdot 2\rvert}{\sqrt{2^2+1^2+(-1)^2}\cdot\sqrt{1^2+(-1)^2+2^2}}\\[15pt] &=\frac{\lvert-1\rvert}{\sqrt{6}\cdot\sqrt{6}}= \frac{1}{6}\\[15pt] \Rightarrow \varphi &=cos^{-1}\left(\frac{1}{6}\right)\approx \underline{80,41}° \end{aligned}\]

Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen