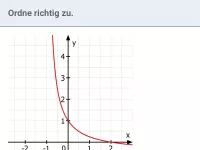
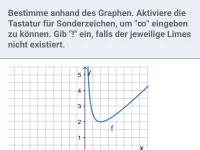
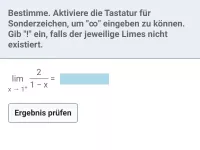
Was passiert mit einem Bruch, wenn der Zähler konstant ≠ 0 ist und der Nenner gegen 0 strebt?

Strebt bei einem Bruch der Zähler gegen eine konstante Zahl ≠ 0 und der Nenner gegen 0- bzw. 0+, so strebt der Bruch, je nach Vorzeichen des Zählers, gegen -∞ oder +∞.
Beispiel
Bestimme, wenn möglich:
l i m
x → 5-   
 
1
−
x
x
−
5
 
          
 
l i m
x → 5   
 
1
−
x
x
−
5
Lösung:
l i m
x → 5-   
 
1
−
x
x
−
5
=
"
 
−
4
0
−
 
"
=
∞
Erläuterung:
  • Der Bruchwert ist positiv, da Zähler und Nenner jeweils negativ sind.
  • Der in Anführungszeichen geschriebene Ausdruck ist nur eine Denkhilfe und darf nicht als Term verstanden werden (0 im Nenner!).
  • Es kann auch helfen, wenn man sich für x → 5- die Folge 4,9; 4,99; 4,999... vorstellt. Setzt man diese Werte der Reihe nach für x ein, erhält man immer größere Bruchwerte, daher ergibt sich ∞ als Ergebnis.
l i m
x → 5   
 
1
−
x
x
−
5
 
   existiert dagegen nicht.
Erläuterung:
  • Im Unterschied zu oben strebt x nicht einseitig gegen 5. Somit kann man im (symbolischen) Nenner weder 0- noch 0+ schreiben.
  • Anders erklärt: Stellt man sich für x → 5 z.B. die Folge 4,9; 5,01; 4,999; 5,0001... vor, so erhält man zwar betragmäßig immer größere Bruchwerte, diese aber abwechselnd positiv und negativ (unbestimmte Divergenz).
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen