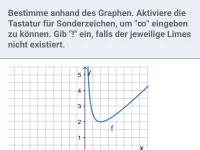
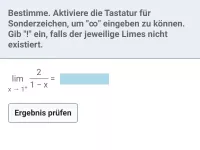
Wie bestimmt man das Verhalten einer gebrochen-rationalen Funktion für x gegen Unendlich?
Der Limes einer gebrochen-rationalen Funktion für x → ∞ oder x → -∞ kann durch Ausklammern der höchsten Nennerpotenz bestimmt werden.
Noch einfacher geht es mit folgender Regel ("z" steht für Zählergrad, "n" für Nennergrad, mit " lZ" und " lN" sind die jeweiligen Leitkoeffizienten gemeint):
- = 0, falls z < n (x- Achse als Asymptote)
- = lZ : lN, falls z = n (waagrechte Asymptote, aber nicht die x-Achse)
- = ∞ bzw. -∞, falls z > n; ob "+" oder "-" findet man heraus, indem man Zähler und Nennergrad sowie die Leitkoeffizienten betrachtet
Beispiel
| = | ? |
Lösung: Man klammert die größte Nennerpotenz (also x²) im Zähler wie im Nenner aus und kürzt anschließend mit dieser. Jetzt kann man -∞ an die Stelle von x setzen (in Anführungszeichen!):
| = | -∞ |
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was sind Polstellen bei gebrochen-rationalen Funktionen und wie verhält sich der Graph in ihrer Umgebung?
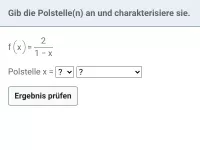
- Wie bestimmt und spezifiziert man eine Polstelle in der Mathematik?
- Was versteht man unter einer behebbaren Definitionslücke?
- Was bedeutet der Limes von f(x) für x → c− bzw. x → c+?
- Was passiert mit einem Bruch, wenn der Zähler konstant ≠ 0 ist und der Nenner gegen 0 strebt?
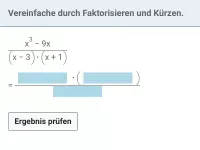
- Wie lassen sich Bruchterme vereinfachen und welche Techniken sind dabei hilfreich?