Was versteht man unter der Rückwärtsversion der binomischen Formeln und welchen Zweck erfüllt diese?
Die drei Binomischen Formeln (BF) lauten in der Rückwärtsversion:
- a² + 2ab + b² = (a + b)²
- a² − 2ab + b² = (a − b)²
- a² − b² = (a + b) (a − b)
In dieser Richtung (links ohne Klammer, rechts mit) ermöglichen die Formeln, eine Summe oder Differenz in ein Produkt umzuformen ("faktorisieren"). Hier ist es wichtig, dass man den linken Term erst einmal überprüft: Liegt die passende Struktur für eine BF vor? Eine Probe (andere Richtung) gibt Gewissheit.
Beispiel 1
Faktorisiere (wenn möglich).
| = | ? |
Überlegung: Es handelt sich um eine einfache Differenz ohne "Mittelterm", also kann man die 3. BF anwenden. Dazu sollten Minuend und Subtrahend zunächst als Quadrate dargestellt werden:
| = |
|
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
| = | ? |
Überlegung: Wenn überhaupt, kommt die 1. BF in Frage. Das Ergebnis wäre dann:
| = |
|
Mittelterm überprüfen:
| = |
|
Also |
|
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
| = | ? |
Überlegung: Wenn überhaupt, kommt die 2. BF in Frage. Das Ergebnis wäre dann:
| = |
|
Mittelterm überprüfen:
| = |
|
Also ist keine Faktorisierung mit Hilfe der BF möglich.
Das Video behandelt weitere Beispiele.

Lernvideo
BINOMISCHE FORMELN rückwärts anwenden einfach erklärt – faktorisieren, Beispiele
Kanal: MathemaTrick
Beispiel 2
Löse durch Faktorisieren:
| = | 0 |
Lösung: Der linke Term kann mit Hilfe der 3. BF faktorisiert werden, denn
| . Forme also um: |
| = | 0 |
Nachdem ein Produkt 0 ist, wenn mindestens ein Faktor 0 ist, gibt es zwei Lösungen:
| = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈9. Klasse - Aufgaben + Stoff + Video
Binomische Formeln
Anwendung Binomischer Formeln zum Multiplizieren von Klammertermen, Faktorisieren, Rationalmachen des Nenners -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Gleichungen - Lösungstechniken
Unterschiedliche Lösungsmethoden quadratischer Gleichungen, u.a. mit Lösungsformel; Ermittlung quadratischer Gleichungen anhand der vorgegebenen Lösung(en); Bruchgleichungen, die auf quadratische Gleichungen zurückgeführt werden können -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratwurzeln - Termumformung mit Binomischen Formeln
Anwendung Binomischer Formeln zum Multiplizieren von Klammertermen, Faktorisieren, Rationalmachen des Nenners
Ähnliche Themen
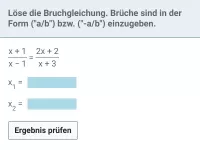
- Ein Zwischenziel beim Lösen einer Bruchgleichung ist, diese nennerfrei zu machen. Wie geht das und auf was sollte man dabei achten, um den Rechenaufwand gering zu halten?
- Gib zwei Spezialfälle quadratischer Gleichungen an, bei denen man auch ohne Lösungsformel weiterkommt. Wie geht man jeweils vor?
- Wie lauten die drei binomischen Formeln?
- Was bedeutet Rationalmachen des Nenners und wie geht man dabei vor?
- Gib jeweils ein Beispiel für eine quadratische Gleichung an, die eine bzw. zwei Lösungen besitzt und begründe dies logisch.
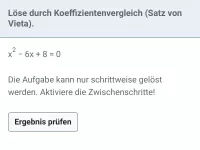
- Wie lautet der Satz von Vieta?
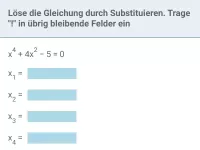
- Wie funktioniert die Lösungsmethode Substitution?
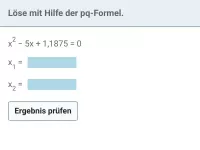
- Erläutere die pq-Formel. Wozu dient sie?
- Wie geht man bei der pq-Formel vor, wenn eine quadratische Gleichung der Art ax² + bx + c = 0 mit a ≠ 1 vorliegt?
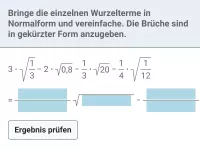
- Was versteht man unter Normalform eines Wurzelterms?