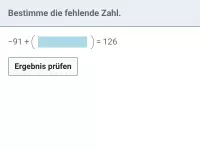
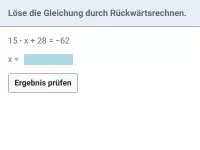
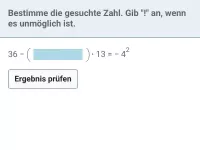
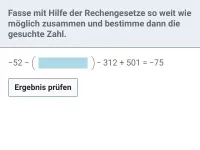
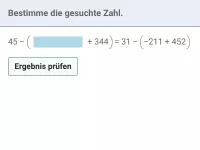
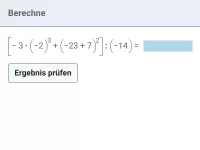
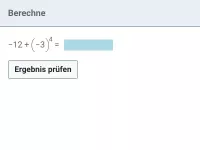
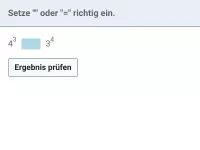
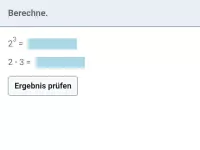
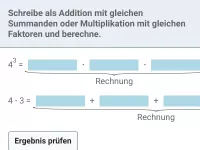
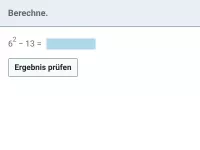
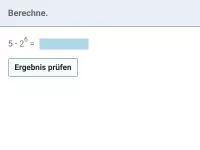
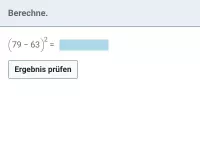
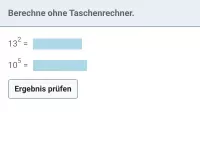
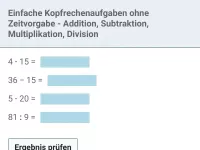
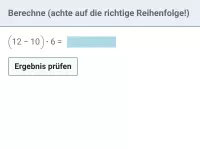
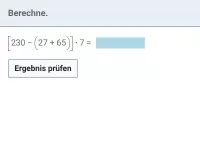
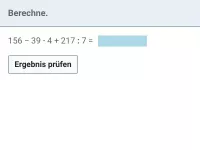
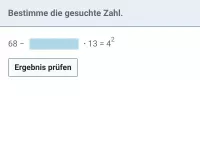
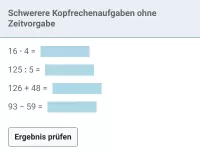
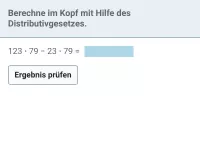
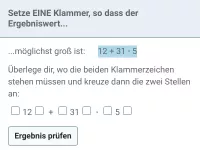
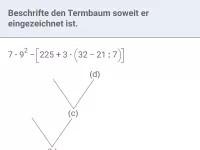
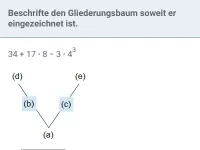
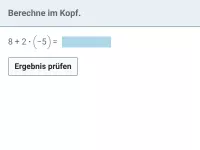
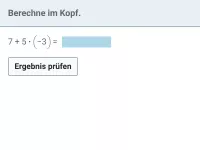
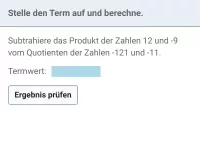
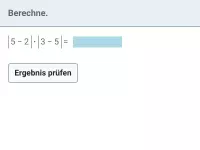
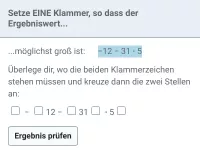
Wie lautet die korrekte Reihenfolge beim Berechnen eines Termwerts?
Klammer vor Potenz vor Punkt (mal und geteilt) vor Strich (plus und minus).
Ansonsten wird von links nach rechts gerechnet!
Beispiel 1
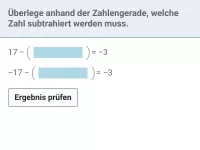
Unterscheide:
| = |
|
| = |
|
Es kommt also darauf an, ob die negative Zahl eingeklammert ist oder nicht.
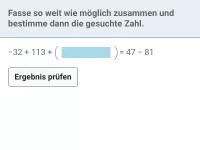
Beispiel 2
| = |
|
- rechts ausrechnen
| = |
|
| = |
|
- Ergebnis der Division
| = |
|
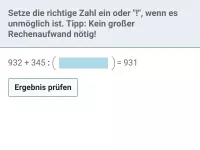
Erklärung: Vom Ergebnis der Division weiß man: addiert man 13 dazu, kommt -8 raus. Die Zahl - 21 erhält man also durch Proberechnung:
| = |
|
- gesuchte Zahl
Der Quotient aus ? und −3 ist also −21. Damit erhält man die gesuchte Zahl durch Proberechnung:
| = |
|
Beispiel 3
|
|
| = |
| Potenz berechnet | |||||
|
| = |
| Endergebnis | |||||
|
|
| = |
| Potenz berechnet | |||||
|
| = |
| Endergebnis | |||||
Beispiel 4
| 2 |
|
| = |
| Klammer berechnet | ||||
|
| = |
| Endergebnis | ||||
| 2 |
|
| = |
| Klammer berechnet | ||||
|
| = |
| Endergebnis | ||||
Beispiel 5
|
|
| = |
| Potenz berechnet | |||||
|
| = |
| Endergebnis | |||||
|
|
| = |
| Potenz berechnet | |||||
|
| = |
| Endergebnis | |||||
Beispiel 6
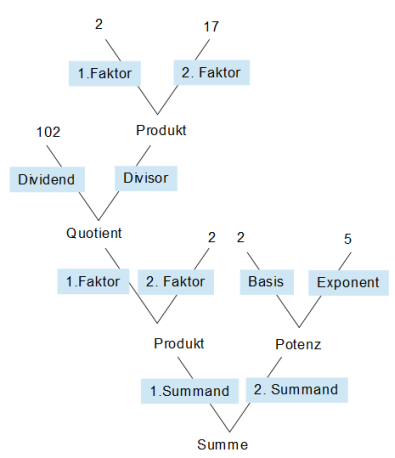
Erstelle einen Gliederungsbaum zu folgendem Term:
| + |
|
Lösung: Der gegliederte Term lautet:
| |||||||||||||||||||||||||||||||||
|
Beachte, dass ZUERST 102 durch das Ergebnis der runden Klammer, also 34 zu teilen ist und ERST DANN die Multiplikation mit 2 erfolgt. Warum? Weil von links nach rechts gerechnet wird, solange nur Punktrechnung auftritt.
Mit dieser Vorarbeit kann nun der Gliederungsbaum erstellt werden:
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈5. Klasse - Aufgaben + Stoff
Einfache Gleichungen in ℤ
Gleichungen im Bereich der ganzen (also auch negativen) Zahlen, die durch Ausprobieren und Rückwärtsrechnen ("Probe") zu lösen sind. -
≈5. Klasse - Aufgaben + Stoff
Potenzen mit negativer ganzzahliger Basis
Potenzen berechnen, Größenvergleich, einfache Gleichungen, Rechnen mit Potenzen -
≈5. Klasse - Aufgaben + Stoff + Video
Potenzen mit positiver Basis
Unterscheidung zwischen Produkt und Potenz, Rechnen mit Potenzen, insbesondere Quadratzahlen -
≈5. Klasse - Aufgaben + Stoff + Video
Verbindung der Grundrechenarten in ℕ - Rechnungen
Punkt vor Strich, Distributivgesetz, Textaufgaben -
≈5. Klasse - Aufgaben + Stoff + Video
Verbindung der Grundrechenarten in ℕ - Terme
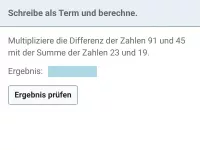
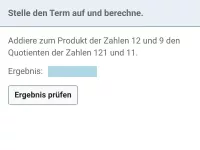
Terme nach Anleitung bilden und berechnen, Termbaum erstellen, Terme durch Klammern manipulieren -
≈5. Klasse - Aufgaben + Stoff
Verbindung der Grundrechenarten in ℤ
Kombination aus Addition, Subtraktion, Multiplikation, Division, Potenzrechnung unter Beachtung der Rechenreihenfolge, insbesondere Klammern; Textaufgaben
Ähnliche Themen
- Wie verändert sich die Position auf der Zahlengerade durch das Addieren einer ganzen Zahl?
- Wie verändert sich die Position auf der Zahlengerade bei Subtraktion einer ganzen Zahl?
- Wann bewegt man sich auf der Zahlengerade durch Strichrechnung nach rechts?
- Wie ist die korrekte Rechenreihenfolge bei Termen mit Addition und Subtraktion?
- Welche Regeln gelten für das Multiplizieren und Dividieren mit den Zahlen 0 und 1?
- Wie schreibt man die Potenz 2^3 als Produkt und welcher Fehler ist dabei zu vermeiden?
- Was besagt das Distributivgesetz in der Mathematik?
- Was bedeutet Ausklammern und welches Rechengesetz wird dabei angewendet?
- Wie ist die Rechenreihenfolge bei gemischter Verwendung von Strich- und Punktrechnung?
- Wie verwendet man das Gleichheitszeichen und das Ungleichheitszeichen?
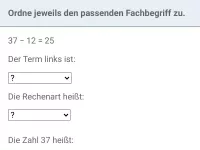
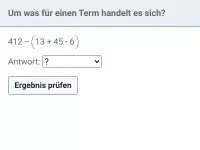
- Welche Fachbegriffe gibt es für die vier Grundrechenarten und ihre Terme sowie Termbestandteile?
- Wie löst man lineare Gleichungen der Form a·x + b = c und a·x - b = c?
- Wie lautet das Distributivgesetz in umgekehrter Form, bei der Summen oder Differenzen in Produkte oder Quotienten umgewandelt werden?
- Was sind die Quadratzahlen von 11 bis 20 und wie berechnet man sie?
- Was ist eine Potenz, wie 4^3, und welche Begriffe sind damit verbunden? Was ergibt 4^0?
- Wie bestimmt man das Vorzeichen von Potenzen mit negativer Basis und begründe die Regel?
- Wie beeinflussen Betragstriche die Berechnung eines Termwerts?