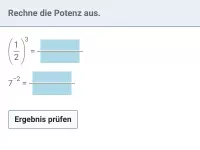
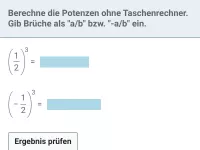
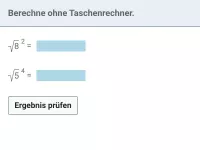
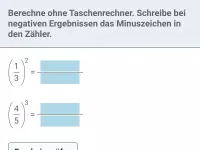
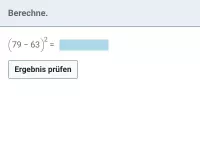
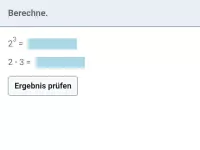
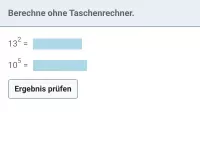
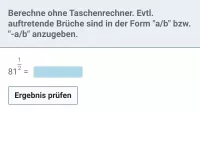
Potenzieren, Mathe-Aufgaben
Potenzieren, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen.
Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 588 Schulen verwendet wird.
Viele unterschiedliche Mathe-Aufgaben und Mathe-Übungen zu 291 Themen der Schulmathematik.

-
≈Oberstufe - Aufgaben + Stoff + Video
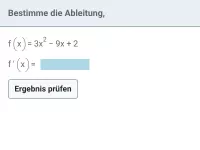
Ableitung - Potenzfunktion - ganzzahliger Exponent
Ableitung von Potenzfunktionen mit ganzzahligem Exponent und ganzrationalen Funktionen (Summen- und Faktorregel); betrachtet werden auch Funktionen mit Parametern -
≈6. Klasse - Aufgaben + Stoff
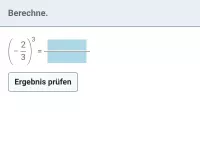
Brüche - Potenzen
Potenz von Brüchen und gemischten Zahlen, Potenzwerte mit negativen ganzzahligen Exponenten -
≈9. Klasse - Aufgaben + Stoff
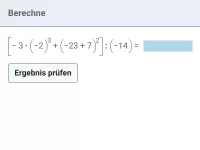
Potenzen - vermischte Aufgaben
Als Basis kommen hier auch irrationale Zahlen, als Exponent auch negative Brüche vor. -
≈8. Klasse - Aufgaben + Stoff
Potenzen mit negativen ganzzahligen Exponenten
Potenzen mit negativer Hochzahl richtig interpretieren und berechnen -
≈5. Klasse - Aufgaben + Stoff
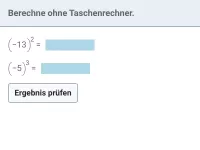
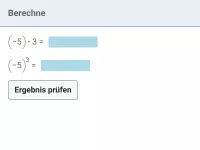
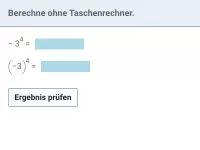
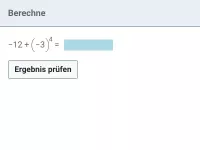
Potenzen mit negativer ganzzahliger Basis
Potenzen berechnen, Größenvergleich, einfache Gleichungen, Rechnen mit Potenzen -
≈5. Klasse - Aufgaben + Stoff + Video
Potenzen mit positiver Basis
Unterscheidung zwischen Produkt und Potenz, Rechnen mit Potenzen, insbesondere Quadratzahlen -
≈9. Klasse - Aufgaben + Stoff
Potenzen mit rationalen Exponenten
n-te Wurzel und Kehrbruch mit Hilfe von Potenzen ausdrücken, Umwandlung zwischen beiden Darstellungsformen, Lösen von Gleichungen durch geeignete Potenzierung -
≈Oberstufe - Aufgaben + Stoff + Video
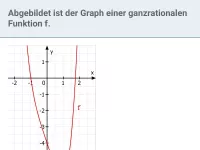
Potenzfunktionen - rationaler Exponent
Definitionsmenge, Graph und Umkehrfunktion von Potenzfunktionen mit rationalem Exponent -
≈9. Klasse - Aufgaben + Stoff
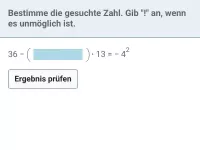
Potenzgleichungen
Einfache Potenzgleichungen und -ungleichungen lösen
Fragen und Antworten zum Thema "potenzieren"
- Wie schreibt man die Potenz 2^3 als Produkt und welcher Fehler ist dabei zu vermeiden?
- Wie lautet die korrekte Reihenfolge beim Berechnen eines Termwerts?
- Wie kann man Potenzen mit negativen oder gebrochenen Exponenten in natürliche Exponenten umformen?
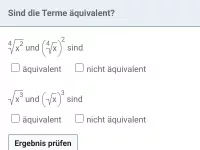
- Wann gelten zwei Terme als äquivalent?
- Wie kann man die Gleichung T(x)^r = a lösen und wann gibt es keine Lösung?
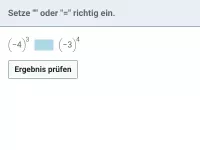
- Wie verwendet man das Gleichheitszeichen und das Ungleichheitszeichen?
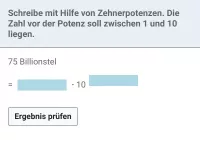
- Was versteht man unter der wissenschaftlichen Notation einer Zahl?
- Was sind die Quadratzahlen von 11 bis 20 und wie berechnet man sie?
- Was ist eine Potenz, wie 4^3, und welche Begriffe sind damit verbunden? Was ergibt 4^0?
- Wie bestimmt man das Vorzeichen von Potenzen mit negativer Basis und begründe die Regel?
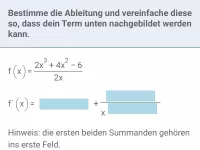
- Wie kann ein gebrochen rationaler Term in eine ganzrationale Form umgewandelt werden und welchen Vorteil hat das beim Ableiten?
- Wie lautet die Ableitung von f(x) = a·x^m und welche zwei Spezialfälle gibt es dazu?
- Wie hängt die maximale Definitionsmenge einer Potenzfunktion von ihrem Exponenten ab?
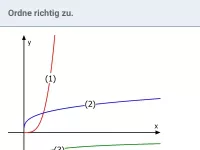
- Welche Klassen von Potenzfunktionen f(x) = x^r, r ∈ ℚ, lassen sich graphisch unterscheiden?
- Was folgt für die Ableitung und jede Stammfunktion einer ganzrationalen Funktion mit ungeradem Grad und negativem Leitkoeffizienten?
- Wie bestimmt man den Term der Umkehrfunktion einer umkehrbaren Funktion?
- Was bedeutet eine Potenz mit negativer Hochzahl, z.B. \(2^{-3}\)?