Anwendungen, Mathe-Aufgaben
Anwendungen, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen.
Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 490 Schulen verwendet wird.
Viele unterschiedliche Mathe-Aufgaben und Mathe-Übungen zu 271 Themen der Schulmathematik.
-
≈5. Klasse - Aufgaben + Stoff
Addition und Subtraktion in ℤ - Anwendungen
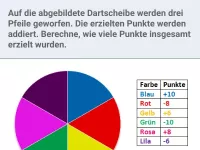
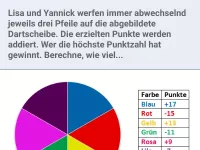
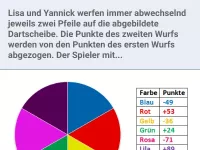
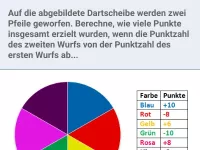
Werfen auf die Dartscheibe, die Punkte der getroffenen Felder werden nach verschiedenen Regeln addiert und subtrahiert. -
≈6. Klasse - Aufgaben + Stoff
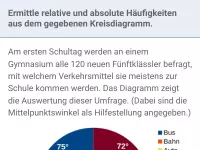
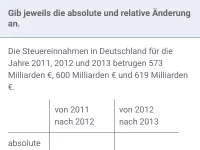
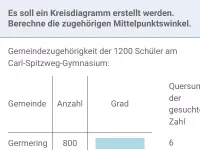
Daten und Diagramme - absolute und relative Häufigkeit
Bestimmung der absoluten und relativen Häufigkeit - letztere dargestellt als Bruch und/oder Prozentsatz -
≈10. Klasse - Aufgaben + Stoff + Video
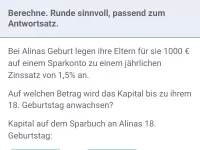
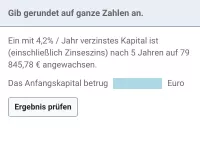
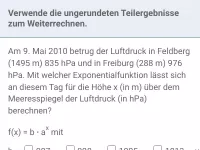
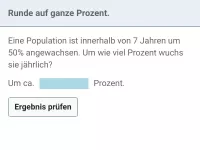
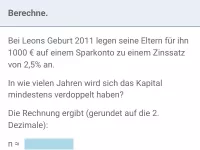
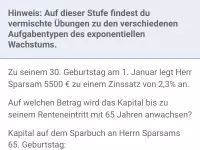
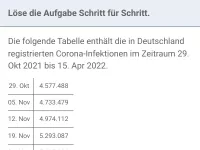
Exponentielles Wachstum - Anwendungen
Exponentielles Wachstum im Sachzusammenhang, Sachaufgaben -
≈5. Klasse - Aufgaben + Stoff
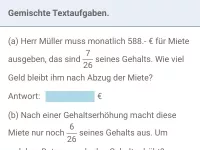
Gemischte Textaufgaben in ℕ und ℤ
Textaufgaben im Bereich der natürlichen und ganzen Zahlen; neben dem Rechnen mit negativen Zahlen sollte man sich auch mit Größeneinheiten sowie mit Teilern und Vielfachen auskennen -
≈6. Klasse - Aufgaben + Stoff + Video
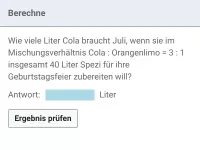
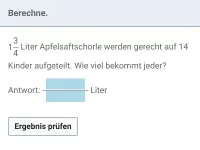
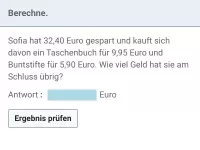
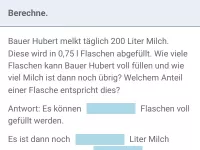
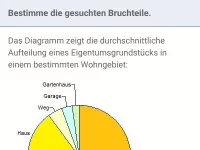
Gemischte Textaufgaben in ℚ (Brüche usw.)
Textaufgaben, bei denen Brüche, Dezimalzahlen und/oder Prozente vorkommen, zum Teil auch Diagramme -
≈7. Klasse - Aufgaben + Stoff
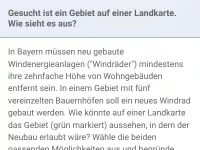
Konstruktion mit Zirkel und Lineal - Anwendungen
Mittelsenkrechte, Lot und Winkelhalbierende in Anwendungssituationen -
≈Oberstufe - Aufgaben + Stoff
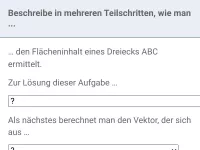
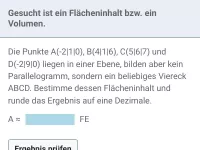
Koordinatengeometrie im Raum - vermischte Aufgaben und Anwendungen
Abstand, Winkel, Lagebeziehung, Fläche und Volumen sowie Spiegelung geometrischer Objekte (Punkt, Gerade, Ebene, Kugel, Pyramide, Prisma) in vermischten Aufgaben und Anwendungen - von Standardverfahren hin zu anspruchsvollen Problemstellungen -
≈7. Klasse - Aufgaben + Stoff + Video
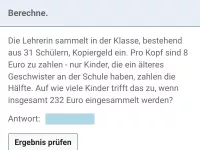
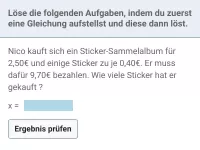
Lineare Gleichungen - Anwendungen
Textaufgaben, die per Aufstellen einer geeigneten linearen Gleichung zu lösen sind. -
≈8. Klasse - Aufgaben + Stoff + Video
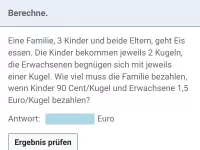
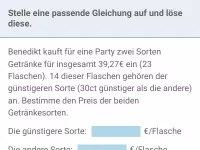
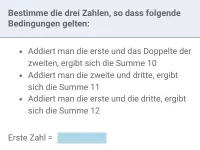
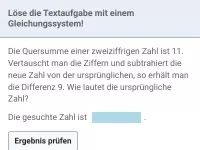
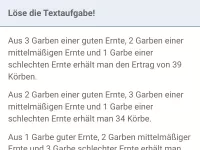
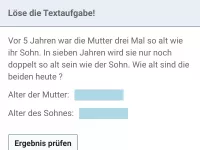
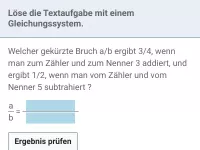
Lineare Gleichungssysteme - Anwendungen
Textaufgaben, die sich mittels linearer Gleichungssysteme lösen lassen (z.B. Mischaufgaben) -
≈9. Klasse - Aufgaben + Stoff
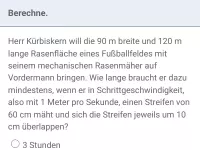
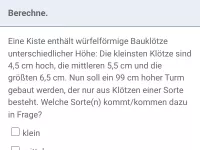
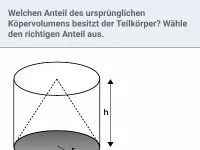
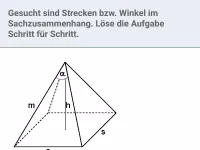
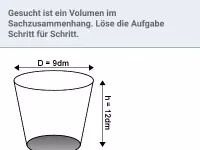
Raumgeometrie - Anwendungen
Innermathematische und sachbezogene Anwendungsaufgaben zu den räumlichen Körpern Prisma, Pyramide, Zylinder und Kegel (in Bezug auf Volumen, Oberfläche, Winkel und Streckenlängen) -
≈8. Klasse - Aufgaben + Stoff
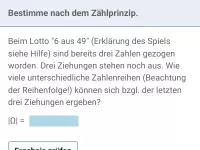
Stochastik - Wahrscheinlichkeit - Zählprinzip
Laplace-Wahrscheinlichkeiten mit Hilfe des Zählprinzips bestimmen
Fragen und Antworten zum Thema "Anwendungen"
- Wie verändert sich die Position auf der Zahlengerade bei Subtraktion einer ganzen Zahl?
- Was bedeutet das Kürzen eines Bruchs und wie wird es durchgeführt?
- Wie addiert man zwei ganze Zahlen unter Berücksichtigung ihrer Vorzeichen und Beträge?
- Wofür wird das Zählprinzip in der Mathematik verwendet?
- Wie kann das Zählprinzip bei mehrstufigen Zufallsexperimenten angewendet werden? Erkläre dies an einem Beispiel.
- Wie sind ein Kreisdiagramm und ein Säulendiagramm aufgebaut?
- Wie hängen Wachstumsrate und Wachstumsfaktor beim exponentiellen Wachstum zusammen?
- Was ist der allgemeine Term einer Exponentialfunktion und welche Bedeutung haben die Parameter?
- Wie löst man Mischaufgaben mit Hilfe von Gleichungen?
- Was ist der Unterschied zwischen absoluter und relativer Häufigkeit?
- Wie beschreibt man die Änderung des Bestandes bei einem Wachstumsvorgang von einem Zeitschritt zum nächsten?
- Was bleibt beim exponentiellen Wachstum gleich und wie geht man bei typischen Fragestellungen vor?
- Wie berechnet man die Volumina von Prismen, Pyramiden, Zylindern und Kegeln?
- Wie berechnet man die Oberflächen von Prismen, Pyramiden, Zylindern und Kegeln und aus welchen Flächen setzen sie sich zusammen?
- Welche Werkzeuge sind in der Raumgeometrie für den Umgang mit Strecken und Winkeln wichtig?
- Wie berechnet man die Fläche eines n-Ecks und das Volumen von drei- oder vierseitigen Prismen und Pyramiden, wenn die Eckpunkte bekannt sind?
- Wie bestimmt man den Schnittwinkel zwischen zwei Geraden, einer Geraden und einer Ebene sowie zwischen zwei Ebenen?
- Wie bestimmt man die Entfernung von einem Punkt zu einer Geraden und die Lage von Punkten mit gleicher oder bestimmter Entfernung zu geometrischen Objekten?
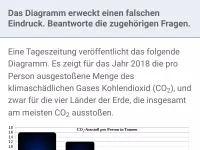
- Wie können Diagramme irreführend sein und welche Tricks werden dabei verwendet?
- Wie liest man absolute und relative Häufigkeiten in Säulendiagrammen ab?
- Wie liest man absolute und relative Häufigkeiten in Kreisdiagrammen ab?
- Wie kann man ein lineares Gleichungssystem mit drei Variablen lösen?
Verwandte Themen
- absolute Häufigkeit
- addieren
- Baumdiagramm
- Daten
- Diagramme
- exponentielles Wachstum
- ganze Zahlen
- Gleichungssysteme
- Kegel
- Kombinatorik
- konstruieren
- lineare Gleichungen
- Mischaufgaben
- natürliche Zahlen
- Oberfläche
- Prisma
- Prozente
- Pyramide
- rationale Zahlen
- Raumgeometrie
- relative Häufigkeit
- Rotationskörper
- Stochastik
- subtrahieren
- Textaufgaben
- Vektorgeometrie
- Volumen
- Zylinder
- Zählprinzip