Infinitesimalrechnung, Mathe-Aufgaben
Infinitesimalrechnung, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen.
Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 588 Schulen verwendet wird.
Viele unterschiedliche Mathe-Aufgaben und Mathe-Übungen zu 291 Themen der Schulmathematik.

-
≈Oberstufe - Aufgaben + Stoff + Video
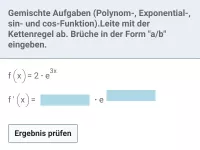
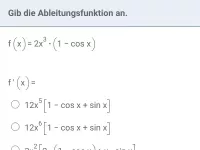
Ableitung - Kettenregel
Kettenregel angewendet auf (Summen von) Potenzfunktionen und trigonometrische Funktionen -
≈Oberstufe - Aufgaben + Stoff + Video
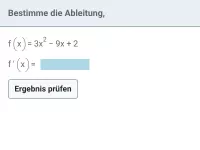
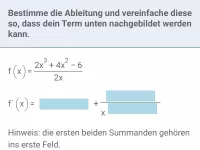
Ableitung - Potenzfunktion - ganzzahliger Exponent
Ableitung von Potenzfunktionen mit ganzzahligem Exponent und ganzrationalen Funktionen (Summen- und Faktorregel); betrachtet werden auch Funktionen mit Parametern -
≈Oberstufe - Aufgaben + Stoff + Video
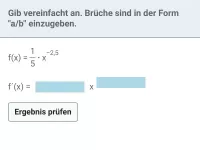
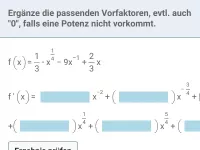
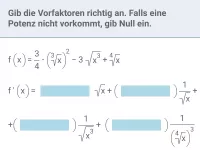
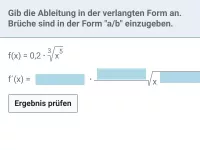
Ableitung - Potenzfunktion - rationaler Exponent
Ableitung von Potenzfunktionen mit rationalem Exponent, wobei die Funktion in Potenz- oder in Wurzelschreibweise vorliegt; betrachtet werden auch Funktionen mit Parametern -
≈Oberstufe - Aufgaben + Stoff + Video
Ableitung - Produkt- und Quotientenregel
Produktregel und Quotientenregel angewendet auf (Summen von) Potenzfunktionen und trigonometrische Funktionen -
≈Oberstufe - Aufgaben + Stoff
Ableitung - trigonometrische Funktionen
Ableitung von sin und cos, verbunden mit Summen- und Faktorregel -
≈Oberstufe - Aufgaben + Stoff
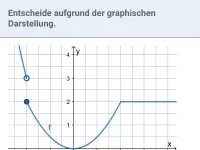
Ableitung und Monotonie
Bestimmung von Monotonieintervallen anhand des Graphen und mit Hilfe der ersten Ableitung -
≈Oberstufe - Aufgaben + Stoff + Video
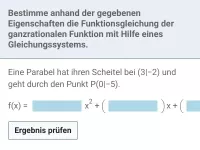
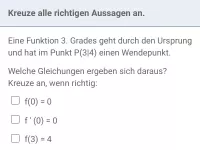
Bestimmung ganzrationaler Funktionen
Bestimmung ganzrationaler Funktionen aufgrund vorgegebener Eigenschaften -
≈Oberstufe - Aufgaben + Stoff + Video
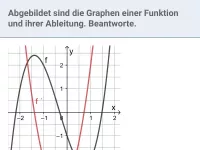
Differenzierbarkeit und Ableitungsfunktion
Untersuchung von abschnittsweise definierten Funktionen und Betragsfunktion auf Differenzierbarkeit; Zusammenhang zwischen f, f´ und F (Stammfunktion) anhand von Graphen -
≈Oberstufe - Aufgaben + Stoff + Video
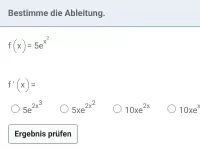
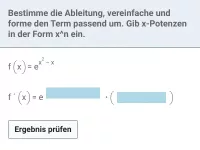
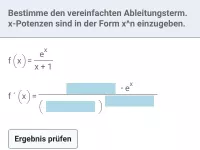
exp und ln - Ableitung
Ableitungsregeln für exp und ln (natürliche Exponentialfunktion/natürliche Logarithmusfunktion), Produkte, Quotienten und Verkettungen von exp und ln mit anderen Funktionen und deren Ableitungen -
≈Oberstufe - Aufgaben + Stoff + Video
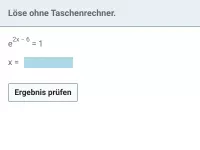
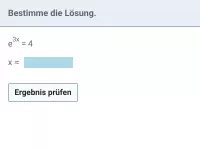
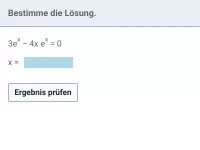
exp und ln - Gleichungen lösen
Gleichungen lösen, die sich auf e^f(x)=b bzw. ln(...)=b zurückführen lassen -
≈Oberstufe - Aufgaben + Stoff + Video
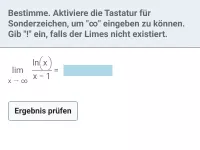
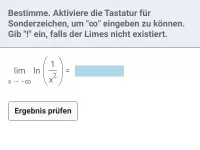
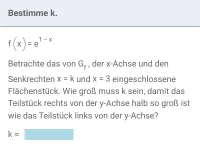
exp und ln - Grenzwertbetrachtungen
Verhalten für x → ∞ und für x → x0 bei Funktionen, die sich u.a. aus exp oder ln zusammensetzen -
≈Oberstufe - Aufgaben + Stoff + Video
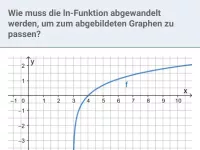
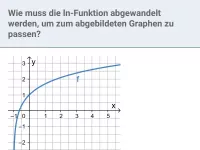
exp und ln - Verschiebung, Streckung und Spiegelung
Spiegelung des Graphen an der x- und y-Achse, Verschiebung in x- und y-Richtung, Streckung und Stauchung -
≈Oberstufe - Aufgaben + Stoff + Video
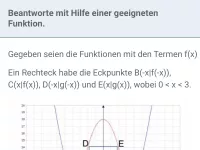
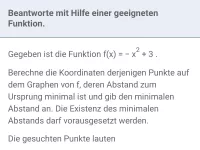
Extremwertaufgaben
Beschreibung vorgegebener Größen (Länge, Fläche, Umsatz, Gewinn) mit Hife von Termen und Berechnung von Minimal- oder Maximalwerten (Optimierung). -
≈Oberstufe - Aufgaben + Stoff + Video
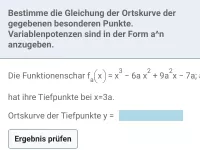
Funktionenschar
Eigenschaften von Funktionenscharen in Abhängigkeit vom Scharparameter -
≈Oberstufe - Aufgaben + Stoff + Video
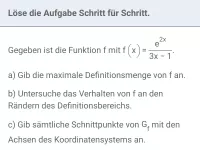
Funktionsuntersuchung - exp und ln
Funktionen und Funktionsscharen, die exp oder ln enthalten, hinsichtlich Dmax, Nullstellen, Verhalten im Unendlichen, Symmetrie des Graphen zum KOSY, relativen Hoch- und Tiefpunkten und weiterer Aspekte untersuchen. -
≈Oberstufe - Aufgaben + Stoff + Video
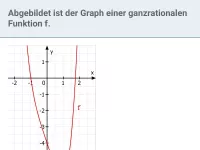
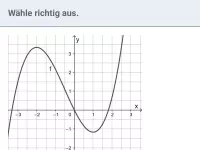
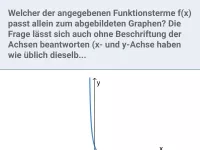
Funktionsuntersuchung - ganzrationale Funktionen
Untersuchung auf Symmetrie zum KOSY, Nullstellen, Verhalten für große |x|, Extrema, Wendepunkte -
≈Oberstufe - Aufgaben + Stoff + Video
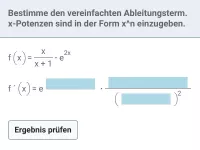
Funktionsuntersuchung - gebrochen-rationale Funktionen
Symmetrie zum KOSY, Nullstellen, Monotonie, Hoch- und Tiefpunkte -
≈Oberstufe - Aufgaben + Stoff + Video
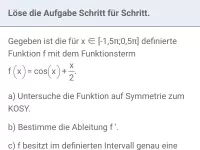
Funktionsuntersuchung - trigonometrische Funktionen
Symmetrie zum KOSY, Nullstellen, Monotonie, Hoch- und Tiefpunkte -
≈Oberstufe - Aufgaben + Stoff + Video
Gebrochen-rationale Funktionen - Funktionsterm und Graph
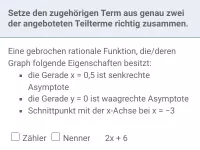
Gebrochen-rationale Funktionen hinsichtlich Definitionsmenge, Polstellen, Nullstellen, Asymptoten untersuchen und den Graph zeichnen; den Term einer gebrochen-rationalen Funktion anhand gegebener Eigenschaften bestimmen -
≈Oberstufe - Aufgaben + Stoff + Video
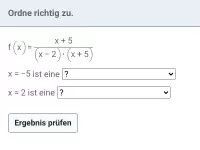
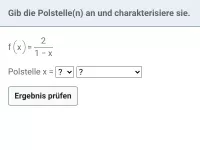
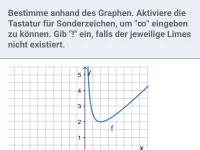
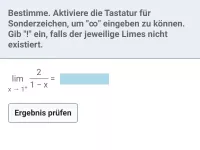
Gebrochen-rationale Funktionen - Polstellen
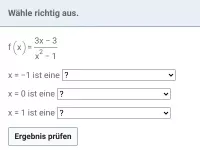
Verhalten von f(x) in der Umgebung von Definitionslücken -
≈Oberstufe - Aufgaben + Stoff + Video
Gebrochen-rationale Funktionen - waagrechte und schräge Asymptoten
Verhalten von f(x) für x→±∞; Bestimmung der Gleichung von waagrechten und schrägen Asymptoten -
≈Oberstufe - Aufgaben + Stoff + Video
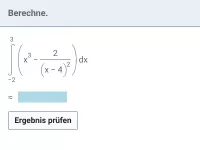
Integral - Berechnung mit Stammfunktion
Stammfunktion von Potenz-, trigonometrischer und natürlicher Exponentialfunktion (auch zusammengesetzt), bestimmtes Integral mit Hilfe von Stammfunktion berechnen -
≈Oberstufe - Aufgaben + Stoff + Video
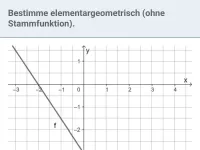
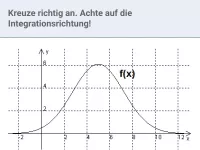
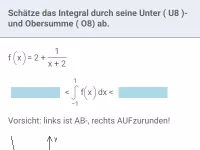
Integral - Betrachtungen ohne Stammfunktion
Integrale grob abschätzen und elementargeometrisch bestimmen, Streifenmethode, Integralfunktion und deren Beziehung zur Integrandenfunktion -
≈Oberstufe - Aufgaben + Stoff + Video
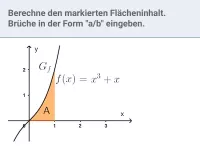
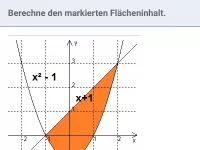
Integral - Flächenberechnung
Bestimmung von Flächen zwischen Graph und x-Achse sowie Flächen zwischen zwei Graphen, auch in Abhängigkeit von Parametern -
≈Oberstufe - Aufgaben + Stoff + Video
Integral - Gesamtänderung einer Größe
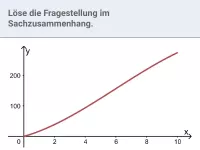
Bedeutung des Integrals über eine Änderungsrate im Sachzusammenhang; Flächenbilanz als Bestandsänderung; graphisch oder rechnerisch von der zeitlichen Änderungsrate auf die Gesamtänderung schließen. -
≈Oberstufe - Aufgaben + Stoff + Video
Integral - Volumen von Rotationskörpern
Interpretation der Rotation eines Graphen um die x-Achse; Volumenberechnungen bei Rotationskörpern; Sachaufgaben mit Rotationskörpern. -
≈Oberstufe - Aufgaben + Stoff + Video
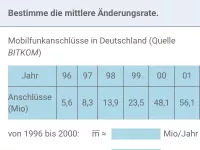
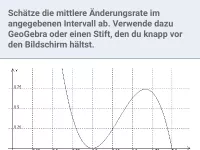
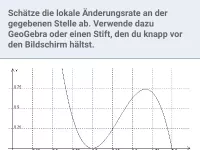
Mittlere und lokale Änderungsrate
Berechnung von mittleren und lokalen (momentanen) Änderungsraten mittels Steigungsdreieck und Differenzenquotient bzw. Differentialquotient -
≈Oberstufe - Aufgaben + Stoff
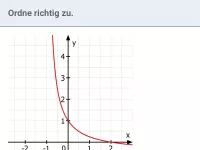
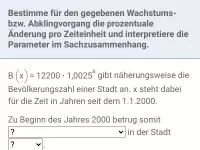
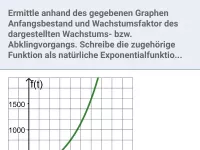
Modellieren von Wachstums- und Abklingvorgängen
Beschreibung von Wachstums- und Abklingvorgängen mit Hilfe der natürlichen Exponentialfunktion; u.a. Ermittlung des Wachstumsfaktors, der Wachstumsgeschwindigkeit, Verdoppelungs- und Halbwertszeit; Basiswechsel von b zu e -
≈Oberstufe - Aufgaben + Stoff
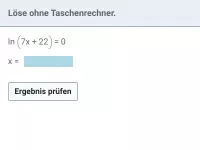
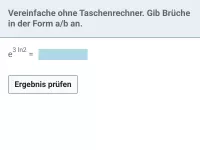
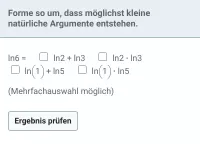
Natürlicher Logarithmus
Rechenregeln, logarithmische Gleichungen -
≈Oberstufe - Aufgaben + Stoff + Video
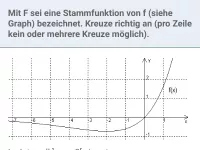
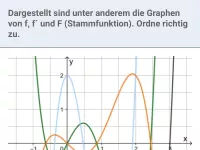
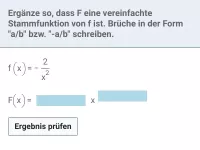
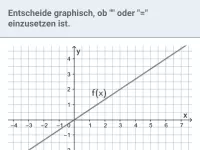
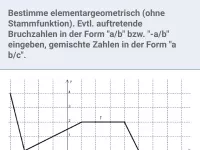
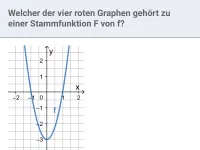
Stammfunktion
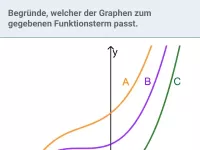
Zeigen, dass F(x) Stammfunktion von f(x) ist; F(x) nach Ableitungsregel (rückwärts) ermitteln; Graphen von F und f einander zuordnen; Eigenschaften von F und f graphisch ermitteln -
≈Oberstufe - Aufgaben + Stoff
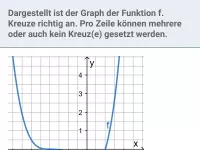
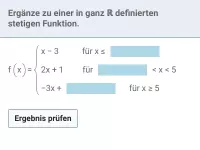
Stetigkeit
Begriff verdeutlichen, abschnittweise definierte Funktion auf Stetigkeit überprüfen bzw. so ergänzen, dass sie stetig ist -
≈Oberstufe - Aufgaben + Stoff + Video
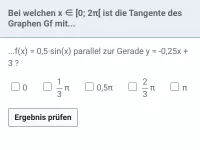
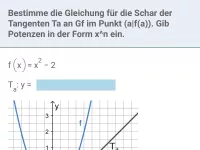
Tangentengleichung und Steigungswinkel
Bestimmung des Steigungswinkels einer Tangente/Normalen an einer vorgegebenen Stelle; Bestimmung der Tangente an einer vorgegebenen Stelle des Graphen bzw. mit vorgegebenen Eigenschaften (Steigung, Steigungswinkel); Bestimmung des Berührpunkts der Tangente, die durch einen bestimmten Punkt geht -
≈Oberstufe - Aufgaben + Stoff
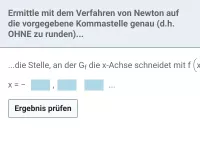
Verfahren von Newton
Annähernde Bestimmung von Nullstellen mit dem Verfahren von Newton -
≈Oberstufe - Aufgaben + Stoff + Video
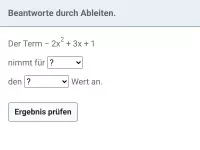
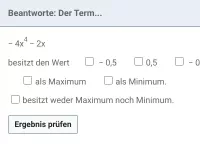
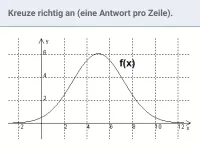
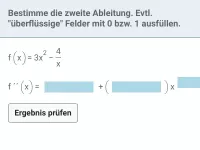
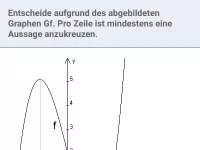
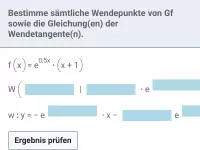
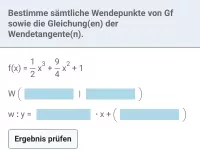
Zweite Ableitung/Krümmung/Wendepunkt
Bestimmung der lokalen Krümmung eines Graphen / maximaler Krümungsintervalle / relativer Extrema mit Hilfe der zweiten Ableitung. Zusammenhang der Graphen von f, f´und f ´´. Bestimmung von Wendepunkten und Wendetangenten.
Fragen und Antworten zum Thema "Infinitesimalrechnung"
- Was sind Polstellen bei gebrochen-rationalen Funktionen und wie verhält sich der Graph in ihrer Umgebung?
- Wie bestimmt und spezifiziert man eine Polstelle in der Mathematik?
- Was versteht man unter einer behebbaren Definitionslücke?
- Wie erkennt man bei gebrochen-rationalen Funktionen die Asymptoten des Graphen?
- Wann und wie wird die Kettenregel in der Mathematik angewendet?
- Was besagt die Produktregel in der Differentialrechnung?
- Was besagt die Quotientenregel in der Differentialrechnung?
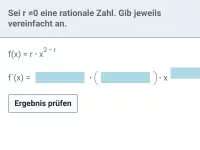
- Wie lautet die Ableitung der Funktion f(x) = a · x^r?
- Wie berechnet man die mittlere Änderungsrate einer Funktion und welcher synonyme Begriff ist dafür gebräuchlich?
- Wie lassen sich die mittlere und lokale Änderungsrate graphisch interpretieren?
- Was ist der Differentialquotient und wie wird er berechnet?
- Unter welchen Bedingungen ist eine Funktion an einer Stelle x=a nicht differenzierbar?
- Was zeigt das Vorzeichen der Ableitung f'(x) einer Funktion an?
- Was ist eine Stammfunktion F von f und welche Beziehung besteht zwischen den Werten von f und F?
- Was versteht man unter der "Ableitungskette" in Bezug auf Funktionen und ihre Graphen?
- Wie lauten die Ableitungen der Funktionen sin(x) und cos(x)?
- Wie funktioniert das Newton-Verfahren zur Nullstellenbestimmung?
- Wie bestimmt man die Steigung der Tangente an einem Punkt eines Graphen?
- Was sind die wesentlichen Aspekte einer vollständigen Funktionsuntersuchung?
- Wie kann eine Funktion f(x) abgewandelt werden, um ihren Graphen Gf zu strecken, stauchen, verschieben oder zu spiegeln?
- Wie erhält man die zweite Ableitung f´´ und unter welchen Bedingungen existiert sie?
- Wie beeinflussen die Vorzeichen von f´ und f´´ den Graphenverlauf von f?
- Wie bestimmt man die Krümmungsintervalle eines Funktionsgraphen?
- Wie kann man mit der zweiten Ableitung feststellen, ob an einer Nullstelle der ersten Ableitung ein relatives Extremum vorliegt und welcher Art es ist?
- Was ist ein Wendepunkt und wie bestimmt man ihn rechnerisch?
- Wie lauten die Ableitungen der Exponentialfunktion und der natürlichen Logarithmusfunktion?
- Was bedeutet der Limes von f(x) für x → c− bzw. x → c+?
- Was passiert mit einem Bruch, wenn der Zähler konstant ≠ 0 ist und der Nenner gegen 0 strebt?
- Wie bestimmt man das Verhalten einer gebrochen-rationalen Funktion für x gegen Unendlich?
- Wie verhält sich die Exponentialfunktion exp(x) für x gegen plus oder minus unendlich?
- Wie verhält sich die natürliche Logarithmusfunktion ln(x) an den Rändern ihres Definitionsbereichs?
- Wie verhalten sich die Funktionen x^n und e^x für x → ∞ und x → −∞?
- Wie verhalten sich der Quotient aus ln(x) und x^n für x → ∞ und das Produkt aus ln(x) und x^n für x → 0^+?
- Wie wird das bestimmte Integral geometrisch interpretiert?
- Was ist eine Integralfunktion und welche Eigenschaften hat sie?
- Wie kann man die Fläche zwischen dem Graphen einer positiven Funktion und der x-Achse in einem Intervall abschätzen und welche Fachbegriffe sind dabei relevant?
- Wie bestimmt man die Fläche zwischen zwei Graphen in einem Intervall, wenn deren Verlauf unbekannt ist?
- Wie berechnet man die Stammfunktion einer Potenzfunktion?
- Wie findet man die Stammfunktion eines Bruchterms, wenn im Zähler die Ableitung des Nenners steht?
- Was sind die Stammfunktionen von exp(x), sin(x) und cos(x) und was ist bei der Integration von f(ax+b) zu beachten?
- Wie bestimmt man die Fläche unter einem Graphen ohne Schnittpunkte mit der x-Achse?
- Wie berechnet man die Fläche zwischen zwei Graphen ohne Schnittpunkte in einem Intervall?
- Wie löst man Optimierungsaufgaben in der Mathematik?
- Wie ist der Zusammenhang zwischen dem Differenzenquotienten und der lokalen Änderungsrate?
- Wie lauten die Produkt- und Quotientenregel der Ableitung?
- Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?
- Was ist eine Funktionenschar und wie berechnet man sie?
- Was ist eine Ortskurve und wie bestimmt man ihre Gleichung?
- Wie bewirkt man durch Änderung des Funktionsterms eine Spiegelung an der x-Achse oder y-Achse sowie eine Verschiebung in y-Richtung?
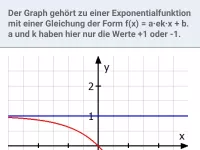
- Wie lautet die Gleichung der Asymptote bei Exponentialfunktionen vom Typ f(x) = a e^(kx) + b?
- Wie funktioniert die Ableitung bei verketteten Funktionen und speziellen Funktionen?
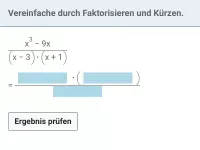
- Wie lassen sich Bruchterme vereinfachen und welche Techniken sind dabei hilfreich?
- Wie kann ein gebrochen rationaler Term in eine ganzrationale Form umgewandelt werden und welchen Vorteil hat das beim Ableiten?
- Wie lautet die Ableitung von f(x) = a·x^m und welche zwei Spezialfälle gibt es dazu?
- Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?
- Wie bestimmt man die lokale Änderungsrate einer Funktion f an der Stelle x_0 mit Differenzenquotienten?
- Was folgt für die Ableitung und jede Stammfunktion einer ganzrationalen Funktion mit ungeradem Grad und negativem Leitkoeffizienten?
- Wie löst man Exponentialgleichungen der Form e^{f(x)} = b?
- Wie löst man Gleichungen der Form ln(...) = b und was ergibt sich, wenn b = 0?
- Was bedeutet es, wenn eine Funktion als stetig oder unstetig bezeichnet wird, und was ist ein Beispiel für eine unstetige Funktion?
- Was versteht man unter einer abschnittweise definierten Funktion und wie prüft man ihre Stetigkeit?
- Wie erkennt man graphisch, dass eine Funktion an einer Stelle nicht differenzierbar ist?
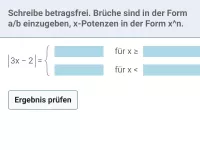
- Wie kann man einen von Betragsstrichen umgebenen Term betragsfrei schreiben?
- Wie ist der Steigungswinkel einer Geraden definiert und wie hängt er mit der Steigung m zusammen?
- Was ist die Normale eines Funktionsgraphen an einem Punkt und wie berechnet man ihre Steigung?
- Was bedeutet "streng monoton steigend/fallend" bei Funktionen?
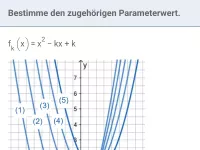
- Wie bestimmt man den Parameterwert k für den Graphen einer Funktionenschar?
- Wie bestimmt man die Funktionsgleichung einer Tangentenschar zu einem Funktionsgraphen?
- Was ist die Ableitung der natürlichen Exponentialfunktion?
- Wie sind die Funktionen e^x und ln(x) miteinander verbunden?
- Wie lautet der Funktionsterm für exponentielles Wachstum und Abklingen und wie bestimmt man die Parameter und die prozentuale Änderung?
- Wie kann man den Funktionsterm eines Wachstums- oder Abklingvorgangs zwischen beliebiger Basis und natürlicher Exponentialfunktion umwandeln?
- Was sind Verdopplungszeit und Halbwertszeit und wie berechnet man sie aus einem Funktionsterm?
- Welche grundlegenden Rechenregeln gelten für Logarithmen?
- Wie wird die Gesamtänderung einer Größe G(t) bei bekannter Änderungsrate G'(t) berechnet?
- Wie entsteht ein Rotationskörper aus dem Graphen einer Funktion und wie berechnet man dessen Volumen?
Verwandte Themen
- ableiten
- Ableitungsfunktion
- Ableitungsregeln
- abschnittsweise definiert
- abschnittweise
- Analysis
- Asymptoten
- Bestandsänderung
- Bestimmung ganzrationaler Funktionen
- Differenzenquotient
- Differenzierbarkeit
- exp
- exponentielles Wachstum
- Extremwerte
- Fläche
- Funktionen mit Parametern
- Funktionenschar
- Funktionsbestimmungen
- ganzzahliger Exponent
- gebrochen-rationale Funktionen
- Gesamtänderung
- Gleichungen
- Halbwertszeit
- Integral
- Kettenregel
- Krümmung
- Kurvendiskussion
- Limes
- ln
- logarithmische Gleichungen
- Modellieren
- Monotonie
- Newton-Verfahren
- Normale
- Nullstellen
- Optimierung
- Ortskurve
- Polstellen
- Polynome
- Potenzen
- Potenzfunktionen
- Produktregel
- Quotientenregel
- rationaler Exponent
- Rechenregeln
- Rotationskörper
- spiegeln
- Sprungstelle
- Stammfunktion
- Steckbriefaufgaben
- Steigungswinkel
- stetig
- strecken
- Streifenmethode
- Tangente
- Tangentenbestimmung
- Terrassenpunkte
- Trigonometrie
- Verdoppelungszeit
- verschieben
- Volumen
- Wachstumsfaktor
- Wachstumsgeschwindigkeit
- Wendepunkte
- Wurzelfunktionen
- zweite Ableitung
- Änderungsrate